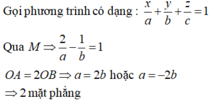Các câu hỏi tương tự
Trong không gian tọa độ Oxyz, cho điểm M(2;-1;0). Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho O A = 2 O B = 3 O C ≠ 0 ?
A. 4
B. 3
C. 2
D. 8
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2) Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x Ox, y Oy, z Oz lần lượt tại các điểm A, B, C sao cho
O
A
O
B
O
C
≠
0
?
A. 3 B. 1 C. 4 D. 8
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2) Hỏi có bao nhiêu mặt phẳng (P) đi qua M và cắt các trục x Ox, y Oy, z Oz lần lượt tại các điểm A, B, C sao cho O A = O B = O C ≠ 0 ?
A. 3
B. 1
C. 4
D. 8
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm
M
1
;
2
;
3
và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC. A.
6
x
+
3
y
−
2
z
−
6
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm M 1 ; 2 ; 3 và cắt các trục Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O). Viết phương trình mặt phẳng (P) sao cho M là trực tâm của tam giác ABC.
A. 6 x + 3 y − 2 z − 6 = 0
B. x + 2 y + 3 z − 14 = 0
C. x + 2 y + 3 z − 11 = 0
D. x 1 + y 2 + z 3 = 3
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M ( 1;2;5) Số mặt phẳng đi qua M và cắt các trục Ox, Oy, Oz tại A, B, C sao cho OA = OB = OC (A, B, C không trùng với gốc tọa độ O) là:
A. 8
B. 3
C. 4
D. 1
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các tia Ox;Oy;Oz lần lượt tại các điểm A, B, C khác gốc tọa độ O sao cho biểu thức 6OA+3OB+2OC có giá trị nhỏ nhất. A.6x+2y+3z-19 0 B. x+2y+3z-14 0 C. x+3y+2z-18 0 D. x+3y+2z-13 0
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các tia Ox;Oy;Oz lần lượt tại các điểm A, B, C khác gốc tọa độ O sao cho biểu thức 6OA+3OB+2OC có giá trị nhỏ nhất.
A.6x+2y+3z-19 = 0
B. x+2y+3z-14 = 0
C. x+3y+2z-18 = 0
D. x+3y+2z-13 = 0
Trong không gian với hệ tọa độ Oxyz. Viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại ba điểm A, B, C khác với gốc tọa độ O sao cho biểu thức
1
O
A
2
+
1
O
B
2
+
1
O
C...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz. Viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt các trục Ox, Oy, Oz lần lượt tại ba điểm A, B, C khác với gốc tọa độ O sao cho biểu thức 1 O A 2 + 1 O B 2 + 1 O C 2 có giá trị nhỏ nhất.
A. P : x + 2 y + 3 z - 14 = 0
B. P : x + 2 y + 3 z - 11 = 0
C. P : x + 2 y + z - 8 = 0
D. P : x + y + 3 z - 14 = 0
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P). A.
3
x
+
2
y
+
z
+
14
0
B.
2
x
+
y
+
3
z
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M(3;2;1). Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
A. 3 x + 2 y + z + 14 = 0
B. 2 x + y + 3 z + 9 = 0
C. 3 x + 2 y + z - 14 = 0
D. 2 x + y + z - 9 = 0
Trong không gian với hệ tọa độ Oxyz. Viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt trục Ox, Oy,Oz lần lượt tại ba điểm A,B,C khác với gốc tọa độ O sao cho biểu thức
1
O
A
2
+
1
O
B
2
+
1
O
C
2
có đạt giá trị nhỏ n...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz. Viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và cắt trục Ox, Oy,Oz lần lượt tại ba điểm A,B,C khác với gốc tọa độ O sao cho biểu thức 1 O A 2 + 1 O B 2 + 1 O C 2 có đạt giá trị nhỏ nhất
A. P : x + 2 y + 3 z - 14 = 0
B. P : x + 2 y + 3 z - 11 = 0
C. P : x + 2 y + z - 14 = 0
D. P : x + y + 3 z - 14 = 0
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) đi qua điểm M (1;2;3) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho
T
1
O
A
2
+
1
O
B
2
+
1
O
C
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) đi qua điểm M (1;2;3) và cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho T = 1 O A 2 + 1 O B 2 + 1 O C 2 đạt giá trị nhỏ nhất.
A. P : x + 2 y + 3 z - 14 = 0
B. P : 6 x - 3 y + 2 z - 6 = 0
C. P : 6 x + 3 y + 2 z - 18 = 0
D. P : 3 x + 2 y + z - 10 = 0