Đáp án C.
Do H là trực tâm tam giác ABC suy ra được H là hình chiếu vuông góc của O trên mặt phẳng (ABC) (học sinh tự chứng minh).
![]()
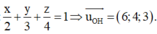
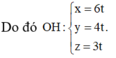
Đáp án C.
Do H là trực tâm tam giác ABC suy ra được H là hình chiếu vuông góc của O trên mặt phẳng (ABC) (học sinh tự chứng minh).
![]()
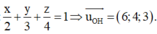
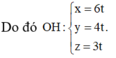
Trong không gian với hệ tọa độ Oxyz , cho ba điểm A(2;0;0), B(0;3;0), C(0;0;4) , mặt phẳng (ABC) có phương trình:
A. x 2 + y 3 + z 4 + 1 = 0
B. x 2 - y 3 + z 4 = 0
C. x 2 + y 3 - z 4 = 0
D. x 2 + y 3 + z 4 = 1
Trong không gian với hệ tọa độ Oxyz, cho các điểm A (2; 0; 0); B (0; 3; 0); C (0; 0 ;4). Gọi H là trực tâm tam giác ABC. Tìm phương trình tham số của đường thẳng OH.
A . x = 4 t y = 3 t z = - 2 t
B . x = 3 t y = 4 t z = 2 t
C . x = 6 t y = 4 t z = 3 t
D . x = 4 t y = 3 t z = 2 t
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(-2;0;0), B(0;3;0) và C(0;0;2). Phương trình nào dưới đây là phương trình của mặt phẳng (ABC)?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(3;0;0), B(0;3;0) và C(0;0;3). Tìm tọa độ trọng tâm G của tam giác ABC.
A. G(3;3;3)
B. G(1;1;1)
C. G(2/3;2/3;2/3)
D. G(1/3;1/3;1/3).
Trong không gian với hệ tọa độ Oxyz, cho các điểm A − 2 ; 0 ; 0 , B 0 ; 4 ; 2 , C 2 ; 2 ; − 2 . Gọi d là đường thẳng đi qua A và vuông góc với mặt phẳng (ABC), S là điểm di động trên đường thẳng d, G và H lần lượt là trọng tâm của tam giác ABC, trực tâm của tams giác SBC. Đường thẳng GH cắt đường thẳng d tại S’. Tính tích SA.S’A’
A. S A . S ' A = 3 2
B. S A . S ' A = 9 2
C. S A . S ' A = 12
D. S A . S ' A = 6
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm A(2;0;0), B(0;3;0), C(0;0;1) Phương trình của α là
![]()
![]()
![]()
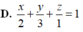
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A 2 ; 3 ; 1 , B − 1 ; 2 ; 0 , C 1 ; 1 ; − 2 . Đường thẳng d đi qua trực tâm của tam giác ABC và vuông góc với mặt phẳng (ABC) có phương trình là
A. x − 1 1 = y + 5 − 8 = z − 4 5 .
B. x − 2 1 = y + 13 − 8 = z − 9 5 .
C. x + 1 1 = y − 11 − 8 = z + 6 5 .
D. x − 3 1 = y + 21 − 8 = z − 14 5 .
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng đi qua các điểm A(2;0;0), B(0;3;0), C0;0;4) có phương trình là:
A. 6x + 4y + 3z + 12 = 0
B. 6x + 4y + 3z = 0
C. 6x + 4y + 3z - 12 = 0
D. 6x + 4y + 3z - 24 = 0
Trong không gian với hệ tọa độ Oxyz cho H(2;1;1). Gọi (P) là mặt phẳng đi qua H và cắt các trục tọa độ tại A; B; C sao cho H là trực tâm tam giác ABC. Phương trình mặt phẳng (P) là:
A. 2x+y+z-6=0
B. x+2y+z-6=0
C. x+2y+2z-6=0
D. 2x+y+z+6=0