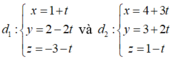Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
x
1
+
t
y
2
-
2
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 x = 1 + t y = 2 - 2 t z = - 3 - t và d 2 x = 4 + 3 t y = 3 + 2 t z = 1 - t . Trên đường thẳng d₁ lấy hai điểm A, B thỏa mã AB=3. Trên đường thẳng d₂ lấy hai điểm C, D thỏa mãn CD=4. Tính thể tích V của tứ diện ABCD.
A. V=7
B. V=2 21
C.V= 4 21 3
D.V= 5 21 6
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng
d
1
:
x
-
1
1
y
+
1
1
z
-
3
-
1
;
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A (1;2;1) và hai đường thẳng d 1 : x - 1 1 = y + 1 1 = z - 3 - 1 ; d 2 : x - 1 1 = y + 2 1 = z - 2 1 . Viết phương trình đường thẳng d song song với mặt phẳng (P):2x+3y+4z-6=0, cắt đường thẳng d1, d2 lần lượt tại M và N sao cho A M ⇀ . A N ⇀ = 5 và điểm N có hoành độ nguyên.
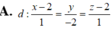
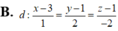
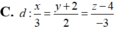
![]()
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD2AB và diện tích bằng 28, đỉnh
A
(
-
1
;
-
1
;
0
)
, phương trình đường thẳng chứa cạnh CD là
x
-
2
2
y
+
1
2...
Đọc tiếp
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD=2AB và diện tích bằng 28, đỉnh A ( - 1 ; - 1 ; 0 ) , phương trình đường thẳng chứa cạnh CD là x - 2 2 = y + 1 2 = z - 3 1 . Tìm tọa độ điểm D biết hoành độ điểm B lớn hơn hoành độ điểm A.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
+
1
-
2
y
-
1
z
-
2
1
và hai điểm A(-1;3;1), B(0;2;-1). Tìm tọa độ điểm C th...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 1 - 2 = y - 1 = z - 2 1 và hai điểm A(-1;3;1), B(0;2;-1). Tìm tọa độ điểm C thuộc d sao cho diện tích của tam giác ABC nhỏ nhất.
A. C(-1;0;2)
B. C(1;1;1)
C. C(-3;-1;3)
D. C(-5;-2;4)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y+z-40 và hai đường thẳng
d
1
:
x
-
3
2
y
-
2
1
z
-
6...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y+z-4=0 và hai đường thẳng d 1 : x - 3 2 = y - 2 1 = z - 6 5 , d 2 : x - 6 3 = y 2 = z - 1 1 . Phương trình đường thẳng d nằm trong mặt phẳng (P) và cắt hai đường thẳng d1, d2 là:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
-
2
1
y
-
5
2
z
-...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A(a;0;0), B(0;0;b). Gọi (P) là mặt phẳng chứa d và d'; H là giao điểm của đường thẳng AA' và mặt phẳng (P). Một đường thẳng D thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d' lần lượt tại B, B'. Hai đường thẳng cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có véc tơ chỉ phương u → = ( 15 ; - 10 ; - 1 ) (tham khảo hình vẽ). Tính T= a+b
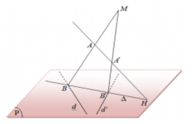
A. T = 8
B. T = 9
C. T = -9
D. 6
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;-2;-3), B(-1;4;1) và đường thẳng
d
:
x
+
2
1
y
-
2
1
z
+
3
2
. Phương trình nào dưới đây là phương trình đường thẳng đi qua trung điểm của đoạn AB v...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai điểm A(1;-2;-3), B(-1;4;1) và đường thẳng d : x + 2 1 = y - 2 1 = z + 3 2 . Phương trình nào dưới đây là phương trình đường thẳng đi qua trung điểm của đoạn AB và song song với d?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d
1
:
x
-
1
2
y
-
1
-
1
z
+
1
1
,
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2;-1;-6) và hai đường thẳng
d 1 : x - 1 2 = y - 1 - 1 = z + 1 1 , d 2 : x + 2 3 = y + 1 1 = z - 2 2 Đường thẳng đi qua điểm M và cắt cả hai đường thẳng d₁, d₂ tại hai điểm A, B. Độ dài đoạn thẳng AB bằng:
A. √38
B. 2√10
C. 8
D. 12
Trong không gian Oxyz, cho mặt cầu (S):
x
2
+
y
2
+
z
2
-
2
x
-
4
y
+
6
z
-
13
0
và đường thẳng ...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2 x - 4 y + 6 z - 13 = 0 và đường thẳng d : x + 1 1 = y + 2 1 = z - 1 1 . Tọa độ điểm M trên đường thẳng d sao cho từ M kẻ được 3 tiếp tuyến MA, MB, MC đến mặt cầu (S) (A, B, C là các tiếp điểm) thỏa mãn A M B ^ = 60 o , B M C ^ = 90 o , C M A ^ = 120 o có dạng M(a;b;c) với a<0. Tổng a+b+c bằng:
A. 2
B. -2
C. 1
D. 10 3