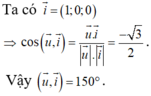Các câu hỏi tương tự
Trong không gian tọa độ Oxyz, góc giữa hai vectơ
i
→
và
u
→
-
3
;
0
;
1
là A. 120°. B. 30°. C. 60°. D. 150°.
Đọc tiếp
Trong không gian tọa độ Oxyz, góc giữa hai vectơ i → và u → = - 3 ; 0 ; 1 là
A. 120°.
B. 30°.
C. 60°.
D. 150°.
Trong không gian với hệ tọa độ Oxyz, biết
u
→
2
;
v
→
1
; và góc giữa hai vectơ
u
→
và
v
→
bằng
2
π
3
. Tìm k để vectơ
p
→
k
u
→
+
v
→
vuôn...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, biết u → = 2 ; v → = 1 ; và góc giữa hai vectơ u → và v → bằng 2 π 3 . Tìm k để vectơ p → = k u → + v → vuông góc với vectơ q → = u → - v → .
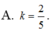
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-2y+z0 và đường thẳng
d
:
x
+
1
1
y
2
z
-
1
. Gọi
∆
là một đường thẳng chứa trong (P) cắt và...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x-2y+z=0 và đường thẳng d : x + 1 1 = y 2 = z - 1 . Gọi ∆ là một đường thẳng chứa trong (P) cắt và vuông góc với d. Vectơ u → = ( a ; 1 ; b ) một vectơ chỉ phương của ∆ . Tính tổng S = a+ b.
A. 1
B. 0
C. 2
D. 4
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;1;-3), B(1;0;-1) và đường thẳng
d
:
x
+
1
2
y
−
2
−
1
z
1
. Đường thẳng d vuông góc với cả hai đường thẳng AB và d thì có vectơ chỉ phương là vectơ nào trong các vectơ dướ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;1;-3), B(1;0;-1) và đường thẳng d : x + 1 2 = y − 2 − 1 = z 1 . Đường thẳng d vuông góc với cả hai đường thẳng AB và d thì có vectơ chỉ phương là vectơ nào trong các vectơ dưới đây?
A. u 1 → = 1 ; − 5 ; 3
B. u 2 → = 1 ; 5 ; 3
C. u 3 → = 4 ; 2 ; 3
D. u 4 → = 3 ; 11 ; 5
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)CH 3. Trong không gian Oxyz cho 2 vectơ a (1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8CH 4.Trong không...
Đọc tiếp
CH 1.Trong không gian Oxyz ; Cho 3 điểm: A(-1; 1; 4) , B(1;- 1; 5) và C(1; 0; 3), toạ độ điểm D để ABCD là một hình bình hành là: A. D(-1; 2; 2) C. D(-1;-2 ; 2) D. D(1; -2; -2)
CH 2.Trong không gian Oxyz cho 2 điểm A (1;–2;2) và B (– 2:0;1). Toạ độ điềm C nằm trên trục Oz để A ABC cân tại C là : A. C(0;0;2) C. C(0;–1;0) B. D(1; 2; -2) В. С(0,:0,-2) D. C( ;0;0)
CH 3. Trong không gian Oxyz cho 2 vectơ a =(1; 2; 2) và (1; 2; -2); khi đó : ¿(i+6) có giá trị bằng : С. 4 A. 10 В. 18 D. 8
CH 4.Trong không gian Oxyz cho 2 vecto a= (3; 1; 2) và b= (2; 0; -1); khi đó vectơ 2a-b có độ dài bằng : А. 3/5 В. 29 С. M D. S/5
CH 5. Cho hình bình hành ABCD với A (-1;0;2), B(3;4;0) D (5;2;6). Tìm khẳng định sai. A. Tâm của hình bình hành có tọa độ là (4;3;3) B. Vecto AB có tọa độ là (4;-4;-2) C. Tọa độ của điểm C là (9;6;4) D. Trọng tâm tam giác ABD có tọa độ là (3;2;2)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
α
: x+y+z-30 và đường thẳng
d
:
x
1
y
+
1
2
z
-
2
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : x+y+z-3=0 và đường thẳng d : x 1 = y + 1 2 = z - 2 - 1 . Gọi ∆ là hình chiếu vuông góc của d trên α và u → = ( 1 ; a ; b ) là một vectơ chỉ phương của ∆ với a, b ∈ ℤ . Tính tổng a+b.
A. 0
B. 1
C. -1
D. -2
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
α
:
x
+
y
+
z
-
3
0
và đường thẳng
d
:
x
1
y
+
1
2
z
-
2
-
1
....
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : x + y + z - 3 = 0 và đường thẳng d : x 1 = y + 1 2 = z - 2 - 1 . Gọi ∆ là hình chiếu vuông góc của d trên α và u → = 1 ; a ; b là một vectơ chỉ phương của ∆ với a , b ∈ ℤ . Tính tổng a+b
A. 0
B. 1
C. - 1
D. - 2
Trong không gian với hệ tọa độ Oxyz, cho
u
→
(1;-2;3). Trong các vectơ sau, đâu là vectơ vuông góc với vectơ
u
→
?
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho u → = (1;-2;3).
Trong các vectơ sau, đâu là vectơ vuông góc với vectơ u → ?
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ
O
x
y
z
, cho hai điểm
A
(
1
;
1
;
-
1
)
,
B
(
2
;
3
;
2
)
. Vectơ
A
B
→
có tọa độ là A.
(
1
;...
Đọc tiếp
Trong không gian với hệ tọa độ O x y z , cho hai điểm A ( 1 ; 1 ; - 1 ) , B ( 2 ; 3 ; 2 ) . Vectơ A B → có tọa độ là
A. ( 1 ; 2 ; 3 )
B. ( - 1 ; - 2 ; 3 )
C. ( 3 ; 5 ; 1 )
D. ( 3 ; 4 ; 1 )