Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz cho A(1;2;3), B(-4;4;6). Tọa độ trọng tâm G cảu tam giác OAB là: A. G(1;-2;-3) B. G(-1;2;3) C. G(-3;6;9) D. G(-3/2;3;9/2).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho A(1;2;3), B(-4;4;6). Tọa độ trọng tâm G cảu tam giác OAB là:
A. G(1;-2;-3)
B. G(-1;2;3)
C. G(-3;6;9)
D. G(-3/2;3;9/2).
Trong không gian với hệ tọa độ Oxyz, cho A(1;2;3), B(0;-2;1), C(1;0;1). Gọi D là điểm sao cho C là trọng tâm tam giác ABD. Tính tổng các tọa độ của D A. 1 B. 0 C.
7
3
D. 7
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho A(1;2;3), B(0;-2;1), C(1;0;1). Gọi D là điểm sao cho C là trọng tâm tam giác ABD. Tính tổng các tọa độ của D
A. 1
B. 0
C. 7 3
D. 7
Trong không gian Oxyz, cho điểm G(1;2;3) là trọng tâm của tam giác ABC trong đó A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz. Tọa độ các điểm A, B, C là: A. A(1; 0; 0), B(0; 2; 0), C(0; 0; 3) B. A(3; 0; 0), B(0; 6; 0), C(0; 0; 9) C. A(-3; 0; 0), B(0; -6; 0), C(0; 0; -9) D. A(6; 0; 0), B(0; 3; 0), C(0; 0; 9)
Đọc tiếp
Trong không gian Oxyz, cho điểm G(1;2;3) là trọng tâm của tam giác ABC trong đó A thuộc trục Ox, B thuộc trục Oy, C thuộc trục Oz. Tọa độ các điểm A, B, C là:
A. A(1; 0; 0), B(0; 2; 0), C(0; 0; 3)
B. A(3; 0; 0), B(0; 6; 0), C(0; 0; 9)
C. A(-3; 0; 0), B(0; -6; 0), C(0; 0; -9)
D. A(6; 0; 0), B(0; 3; 0), C(0; 0; 9)
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;0;1), B (0;1;-1). Hai điểm D, E thay đổi trên các đoạn OA, OB sao cho đường thẳng DE chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi DE ngắn nhất thì trung điểm của đoạn DE có tọa độ là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;0;1), B (0;1;-1). Hai điểm D, E thay đổi trên các đoạn OA, OB sao cho đường thẳng DE chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi DE ngắn nhất thì trung điểm của đoạn DE có tọa độ là:
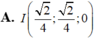

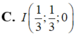
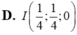
Trong không gian Oxyz, cho hai điểm
A
(
1
;
3
-
5
)
,
B
(
-
3
;
1
;
-
1
)
. Tìm toạ độ trọng tâm G của tam giác OAB
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A ( 1 ; 3 - 5 ) , B ( - 3 ; 1 ; - 1 ) . Tìm toạ độ trọng tâm G của tam giác OAB
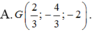
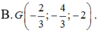
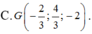
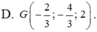
Trong không gian với hệ trục tọa độ Oxyz, cho điểm G(1;2;3). Mặt phẳng
α
đi qua G cắt Ox, Oy, Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm G(1;2;3). Mặt phẳng α đi qua G cắt Ox, Oy, Oz lần lượt tại A, B, C sao cho G là trọng tâm của tam giác ABC. Viết phương trình mặt phẳng
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho tam giác ABC có A(2;3;-1), B(1;3;2), G(2;-3;-1) là trọng tâm của tam giác ABC. Tọa độ của điểm C là: A. (3;-15;-4) B. (-1;-9;-2) C. (-3;15;4) D. (1;9;2)
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC có A(2;3;-1), B(1;3;2), G(2;-3;-1) là trọng tâm của tam giác ABC. Tọa độ của điểm C là:
A. (3;-15;-4)
B. (-1;-9;-2)
C. (-3;15;4)
D. (1;9;2)
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(1;3;5), B(2;0;1), C(0;9;0) Tọa độ trọng tâm G của tam giác ABC là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(1;3;5), B(2;0;1), C(0;9;0) Tọa độ trọng tâm G của tam giác ABC là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A (1;-2;3), B (-1;0;2) và G (1;-3;2) là trọng tâm tam giác ABC. Tìm tọa độ điểm C.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam
giác ABC có A (1;-2;3), B (-1;0;2) và G (1;-3;2)
là trọng tâm tam giác ABC. Tìm tọa độ điểm C.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) cắt Ox tại A, Oy tại B, Oz tại C. Biết G(1;2;3) là trọng tâm của tam giác ABC, xác định phương trình mặt phẳng (P).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) cắt Ox tại A, Oy tại B, Oz tại C. Biết G(1;2;3) là trọng tâm của tam giác ABC, xác định phương trình mặt phẳng (P).
![]()
![]()







