Các câu hỏi tương tự
Trong không gian Oxyz, cho hai mặt phẳng
(
P
)
:
x
-
y
-
6
0
và (Q). Biết rằng điểm
H
(
2
;
-
1
;
-
2
)
là hình chiếu vuông góc của gốc tọa độ
O
(
0
;
0
;
0
)
xuống mặt phẳng (Q). Số đo góc giữa mặt phẳng (P) và mặ...
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng ( P ) : x - y - 6 = 0 và (Q). Biết rằng điểm H ( 2 ; - 1 ; - 2 ) là hình chiếu vuông góc của gốc tọa độ O ( 0 ; 0 ; 0 ) xuống mặt phẳng (Q). Số đo góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho điểm H(2; –1;2) là hình chiếu vuông góc của gốc tọa độ O xuống mặt phẳng (P). Số đo góc giữa mặt phẳng (P) và mặt phẳng (Q) có phương trình – y + z 0 là: A.
90
0
. B.
60
0
. C.
45
0
. D.
30
0
.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm H(2; –1;2) là hình chiếu vuông góc của gốc tọa độ O xuống mặt phẳng (P). Số đo góc giữa mặt phẳng (P) và mặt phẳng (Q) có phương trình – y + z = 0 là:
A. 90 0 .
B. 60 0 .
C. 45 0 .
D. 30 0 .
Trong hệ trục toạ độ Oxyz, cho điểm H(2;1;2). Điểm H là hình chiếu vuông góc của gốc toạ độ O xuống mặt phẳng (P), số đo góc giữa mặt phẳng (P) và mặt phẳng (Q): x+y-110 là A. 90
°
B. 30
°
C. 60
°
D. 45
°
Đọc tiếp
Trong hệ trục toạ độ Oxyz, cho điểm H(2;1;2). Điểm H là hình chiếu vuông góc của gốc toạ độ O xuống mặt phẳng (P), số đo góc giữa mặt phẳng (P) và mặt phẳng (Q): x+y-11=0 là
A. 90 °
B. 30 °
C. 60 °
D. 45 °
Trong không gian Oxyz, cho đường thẳng
d
:
x
-
1
2
m
+
1
y
+
3
2
z
+
1
m
-
2
và mặt phẳng (P) : x + y +z - 6 0. Gọi đường thẳng
∆
là hình chi...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d : x - 1 2 m + 1 = y + 3 2 = z + 1 m - 2 và mặt phẳng (P) : x + y +z - 6 = 0. Gọi đường thẳng ∆ là hình chiếu vuông góc của d lên mặt phẳng (P) . Có bao nhiêu số thực m để đường thẳng ∆ vuông góc với giá của véctơ a → = (-1;0;1)?
A. 2
B. 1
C. 3
D. 0
Trong không gian với hệ tọa độ Oxyz, cho M (3; 4; 5) và mặt phẳng (P): x - y + 2z - 3 0. Hình chiếu vuông góc của M lên mặt phẳng (P) là: A. H (2; 5; 3) B. H (2; -3; 1) C. H (6; 7; 3) D. H (1; 5; 2)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho M (3; 4; 5) và mặt phẳng (P): x - y + 2z - 3 = 0. Hình chiếu vuông góc của M lên mặt phẳng (P) là:
A. H (2; 5; 3)
B. H (2; -3; 1)
C. H (6; 7; 3)
D. H (1; 5; 2)
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(2;0;0) , B(1;-4;0), C(0;-2;6) và mặt phẳng ( α ) : x + 2y + z- 5 = 0. Gọi H(a;b;c) là hình chiếu vuông góc của trọng tâm tam giác ABC lên mặt phẳng ( α ) . Tính P = a - b + c.
A. 5
B. -3
C. 3
D. -1
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (3; 4; 5) và mặt phẳng (P): x - y + 2z - 3 0. Hình chiếu vuông góc của điểm M lên mặt phẳng (P) là: A. H (1; 2; 2) B. H (2; 5; 3) C. H (6; 7; 8) D. H (2; -3; -1)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (3; 4; 5) và mặt phẳng (P): x - y + 2z - 3 = 0. Hình chiếu vuông góc của điểm M lên mặt phẳng (P) là:
A. H (1; 2; 2)
B. H (2; 5; 3)
C. H (6; 7; 8)
D. H (2; -3; -1)
Trong không gian với hệ trục tọa độ Oxyz, cho M(3;4;5) và mặt phẳng (P)x-y+2z-30. Hình chiếu vuông góc của M lên mặt phẳng (P) là A. H(1;2;2) B. H(2;5;3) C. H(6;7;8) D. H(2;-3;-1)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho M(3;4;5) và mặt phẳng (P)x-y+2z-3=0. Hình chiếu vuông góc của M lên mặt phẳng (P) là
A. H(1;2;2)
B. H(2;5;3)
C. H(6;7;8)
D. H(2;-3;-1)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:
x
-
1
1
y
-
1
2
z
-
2
-
1
và mặt phẳng (P): 2x+y+2z-10 Gọi d’ là hình chiếu củ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 1 1 = y - 1 2 = z - 2 - 1 và mặt phẳng (P): 2x+y+2z-1=0 Gọi d’ là hình chiếu của đường thẳng d lên mặt phẳng (P), vectơ chỉ phương của đường thẳng d’ là
![]()
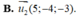
![]()
![]()




