Các câu hỏi tương tự
Cho bốn mệnh đề sau:(1) Nếu hai mặt phẳng
α
v
à
β
song song với nhau thì mọi đường thẳng nằm trong mặt phẳng
α
đều song song với
β
.
(2) Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.(3) Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.(4) Có thể tìm được hai đường thẳng song song mà mỗi đường thẳng cắ...
Đọc tiếp
Cho bốn mệnh đề sau:
(1) Nếu hai mặt phẳng α v à β song song với nhau thì mọi đường thẳng nằm trong mặt phẳng α đều song song với β .
(2) Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.
(3) Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.
(4) Có thể tìm được hai đường thẳng song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trước
Trong các mệnh đề trên có bao nhiêu mệnh đề sai?
A. 4
B. 2
C. 3
D. 1
Cho bốn mệnh đề sau:1) Nếu hai mặt phẳng
α
và
β
song song với nhau thì mọi đường thẳng nằm trong mặt phẳng
α
đều song song với
β
. 2) Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.3) Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.4) Có thể tìm được hai đường thẳng song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trướcTrong...
Đọc tiếp
Cho bốn mệnh đề sau:
1) Nếu hai mặt phẳng α và β song song với nhau thì mọi đường thẳng nằm trong mặt phẳng α đều song song với β .
2) Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.
3) Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.
4) Có thể tìm được hai đường thẳng song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trước
Trong các mệnh đề trên có bao nhiêu mệnh đề sai?
A. 4
B. 2
C. 3
D. 1
Trong không gian, cho các mệnh đề sau:I. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.II. Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.III. Nếu đường thẳng a song song với đường thẳng b, đường thẳng b nằm trên mặt phẳng (P) thì a song song với (P).IV. Qua điểm A không thuộc mặt phẳng
(
α
)
, kẻ được đúng một đường thẳng song song với . Số mệnh đề đúng là A....
Đọc tiếp
Trong không gian, cho các mệnh đề sau:
I. Hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.
II. Hai mặt phẳng phân biệt chứa hai đường thẳng song song cắt nhau theo giao tuyến song song với hai đường thẳng đó.
III. Nếu đường thẳng a song song với đường thẳng b, đường thẳng b nằm trên mặt phẳng (P) thì a song song với (P).
IV. Qua điểm A không thuộc mặt phẳng ( α ) , kẻ được đúng một đường thẳng song song với .
Số mệnh đề đúng là
A. 2
B. 0
C. 1
D. 3
Trong không gian cho các đường thẳng a, b, c và mặt phẳng (P). Mệnh đề nào sau đây sai? A. Nếu a//b và b
⊥
c thì c a B. Nếu a
⊥
b và b
⊥
c thì a//c C. Nếu a
⊥
(P) và b//(P) thì a
⊥
b D. Nếu a
⊥
b, c
⊥
b và a cắt c thì b vuông góc với mặt phẳng chứa a và c
Đọc tiếp
Trong không gian cho các đường thẳng a, b, c và mặt phẳng (P). Mệnh đề nào sau đây sai?
A. Nếu a//b và b ⊥ c thì c a
B. Nếu a ⊥ b và b ⊥ c thì a//c
C. Nếu a ⊥ (P) và b//(P) thì a ⊥ b
D. Nếu a ⊥ b, c ⊥ b và a cắt c thì b vuông góc với mặt phẳng chứa a và c
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;-2;-3); B(1;1;1) và hai đường thẳng
∆
1
:
x
-
2
1
y
-
2
4
z
+
6
-
3
;
...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;-2;-3); B(1;1;1) và hai đường thẳng ∆ 1 : x - 2 1 = y - 2 4 = z + 6 - 3 ; ∆ 2 : x - 2 1 = y + 3 - 4 = z - 4 3 . Gọi m là số mặt phẳng (P) tiếp xúc với mặt cầu đường kính AB đồng thời song song với cả hai đường thẳng ∆1;∆2; n là số mặt phẳng (Q), sao cho khoảng cách từ A đến (Q) bằng 15, khoảng cách từ B đến (Q) bằng 10. Chọn mệnh đề đúng trong các mệnh đề sau.
A. m + n = 1
B. m + n = 4
C. m + n = 3
D. m + n = 2
Cho các mệnh đề sau:(I) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng cùng nằm trong một mặt phẳng.(II) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng có giá song song với một mặt phẳng.(III) 3 vecto
a
→
,
b
→
,
c
→
đồng phẳng nếu tồn tại duy nhất bộ số (m,n) sao cho
a...
Đọc tiếp
Cho các mệnh đề sau:
(I) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng cùng nằm trong một mặt phẳng.
(II) 3 vecto gọi là đồng phẳng khi và chỉ khi chúng có giá song song với một mặt phẳng.
(III) 3 vecto a → , b → , c → đồng phẳng nếu tồn tại duy nhất bộ số (m,n) sao cho a → = m b → + n c → .
Số mệnh đề đúng là:
A. 0
B. 1
C. 2
D. 3
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
-
2
1
y
-
5
2
z
-
2
1
,
d
:
x
-
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A(a;0;0), A’(0;0;b). Gọi (P) là mặt phẳng chứa d và d’; H là giao điểm của đường thẳng AA’ và mặt phẳng (P). Một đường thẳng thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d’ lần lượt tại B, B’. Hai đường thẳng AB, A’B’ cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương u → = 15 ; - 10 ; - 1 (tham khảo hình vẽ). Tính a+b
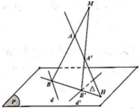
A. 8
B. 9
C. -9
D. 6
Cho hai hàm số
y
e
x
và
y
ln
x
. Xét các mệnh đề sau (I) Đồ thị hai hàm số đối xứng qua đường thẳng yx(II) Tập xác định của hai hàm số trên là R (III) Đồ thị hai hàm số cắt nhau tại đúng một điểm. (IV) Hai hàm số đều đồng biến trên tập xác định của nó.Có bao nhiêu mệnh đề sai trong các mệnh đề trên? A. 2 B. 3 C. 1 D. 4
Đọc tiếp
Cho hai hàm số y = e x và y = ln x . Xét các mệnh đề sau
(I) Đồ thị hai hàm số đối xứng qua đường thẳng y=x
(II) Tập xác định của hai hàm số trên là R
(III) Đồ thị hai hàm số cắt nhau tại đúng một điểm.
(IV) Hai hàm số đều đồng biến trên tập xác định của nó.
Có bao nhiêu mệnh đề sai trong các mệnh đề trên?
A. 2
B. 3
C. 1
D. 4
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
−
2
1
y
−
5
2
z
−
2
1
,
d
:
x
−
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x − 2 1 = y − 5 2 = z − 2 1 , d ' : x − 2 1 = y − 1 − 2 = z − 2 1 và hai điểm A a ; 0 ; 0 , A ' 0 ; 0 ; b . Gọi (P) là mặt phẳng chứa d và d¢; H là giao điểm của đường thẳng AA¢ và mặt phẳng (P). Một đường thẳng D thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d¢ lần lượt tại B, B¢. Hai đường thẳng A B , A ' B ' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có véc tơ chỉ phương u → 15 ; − 10 ; − 1 (tham khảo hình vẽ). Tính T = a + b

A. T = 8
B. T = 9
C. T = - 9
D. T = 6



