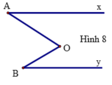
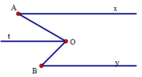
 Qua điểm O kẻ tia Ot // Ox. Khi đó,
A
^
=
A
O
x
^
(2 góc so le trong).
Qua điểm O kẻ tia Ot // Ox. Khi đó,
A
^
=
A
O
x
^
(2 góc so le trong).
Do O t ∥ O x O y ∥ O x nên O t ∥ O y , B ^ = B O t ^ (2 góc so le trong)
Từ đó, ta có A O B ^ = A O t ^ + t O B ^ = A ^ + B ^ .
Vậy A ^ + B ^ = A O B ^ (đpcm)