A = {n ∈ N | n là một ước chung của 24 và 30} = {1; 2; 3; 6}.
B = {n ∈ N | n là một ước của 6} = {1; 2; 3; 6}.
Ta thấy A ⊂ B và B ⊂ A nên A = B.
A = {n ∈ N | n là một ước chung của 24 và 30} = {1; 2; 3; 6}.
B = {n ∈ N | n là một ước của 6} = {1; 2; 3; 6}.
Ta thấy A ⊂ B và B ⊂ A nên A = B.
cho 2 tập hợp A={x\(\in\)R|(x-1)(x-2)(x-4)=0}, B={n\(\in\)N|n là ước của 4}. 2 tập hợp A và B, tập hợp nào là tập con của tập còn lại. 2 tập hợp A và B có bằng nhau không.
Trong hai tập hợp A, B dưới đây, tập hợp nào là tập hợp con của tập còn lại? Hai tập hợp A và B có bằng nhau không?
A là tập hợp các hình vuông;
B là tập hợp các hình thoi.
Cho các tập hợp: A = { m ∈ ℕ | m là ước của 16} } ; B = { n ∈ ℕ | n là ước của 24}. Tập hợp A ∩ B là:
A. ∅
B. { 1 ; 2 ; 4 ; 8 }
C. { ± 1 ; ± 2 ; ± 4 ; ± 8 }
D. { 1 ; 2 ; 4 ; 8 ; 16 }
Cho
A = { n ∈ N | n là ước của 12}
B = { n ∈ N | n là ước của 18}
Liệt kê các phần tử của tập hợp C các ước chung của 12 và 18
Cho tập hợp A = {x ∈ N/x là ước chung của 36 và 120}. Các phần tử của tập A là:
A. A = 1 ; 2 ; 3 ; 4 ; 6 ; 12
B. A = 1 ; 2 ; 3 ; 4 ; 6 ; 8 ; 12
C. A = 2 ; 3 ; 4 ; 6 ; 8 ; 10 ; 12
D. A = 2 ; 3 ; 4 ; 6 ; 12
Các phần tử của tập hợp N = { x ∈ N : x là ước chung của 24 và 36} là
A. {0; 1; 2; 3; 4; 6; 12}.
B. {1; 2; 3; 4; 6}.
C. {0; 1; 2; 3; 4; 6}.
D. {1; 2; 3; 4; 6; 12}.
Cho A và B là hai tập hợp con của tập hợp E được biểu diễn bởi biểu đồ Ven dưới đây
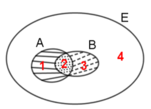
Trong các phát biểu sau
I. Vùng 1 là tập hợp A \ B.
II. Vùng 2 là tập hợp A ∩ B.
III. Vùng 3 là tập hợp B \ A.
IV. Vùng 4 là tập hợp E \ (A ∪ B).
Số phát biểu đúng là:
A. 1.
B. 2.
C. 3.
D. 4.
Cho hai tập hợp A = { a = 3 n | n ∈ ℕ * } , B = { b ∈ ℕ | 0 < b ≤ 9 } .
Khẳng định nào dưới đây là không đúng?
A. A ∩ B = { 3 ; 6 ; 9 }
B. B ⊂ A
C. 15 ∈ A ,15 ∉ B
D. 18 ∈ A ,9 ∈ A ,9 ∈ B
Cho hai tập hợp A = { x x là ước số nguyên dương của 12}.
B = { x x là ước số nguyên dương của 18}
Tập hợp A B là:
A. 0 ; 1 ; 2 ; 3 ; 6
B. 1 ; 2 ; 3 ; 4
C. 1 ; 2 ; 3 ; 6
D. 1 ; 2 ; 3