Các câu hỏi tương tự
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu). A.
2
a
2
3...
Đọc tiếp
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu).
A. 2 a 2 3
B. a 2 2 3
C. a 2 4
D. a 2 4 3
Cho hình trụ (T) có MN , PQ vuông góc với nhau lần lượt là hai đường kinh nằm trên hai đường tròn đáy của hình trụ. Thể tích khối tứ diện MNPQ bằng 10. Tính thể tích của khối trụ (T). A. 60
π
B. 30
π
C. 45
π
D. 15
π
Đọc tiếp
Cho hình trụ (T) có MN , PQ vuông góc với nhau lần lượt là hai đường kinh nằm trên hai đường tròn đáy của hình trụ. Thể tích khối tứ diện MNPQ bằng 10. Tính thể tích của khối trụ (T).
A. 60 π
B. 30 π
C. 45 π
D. 15 π
Lăng trụ tứ giác đều có độ dài tất cả các cạnh bằng nhau và có diện tích toàn phần bằng
6
a
2
. Thể tích khối lăng trụ đã cho bằng
Đọc tiếp
Lăng trụ tứ giác đều có độ dài tất cả các cạnh bằng nhau và có diện tích toàn phần bằng 6 a 2 . Thể tích khối lăng trụ đã cho bằng
![]()
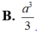
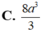
![]()
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng A.
7
6
B.
11
12
C.
2
3
D.
5
6
Đọc tiếp
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng
A. 7 6
B. 11 12
C. 2 3
D. 5 6
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng. DE Thể tích của khối đa diện ABCDSEF bằng:
Đọc tiếp
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng. DE Thể tích của khối đa diện ABCDSEF bằng:
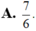
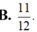
![]()
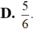
Cho lăng trụ tứ giác đều có tất cả các cạnh bằng nhau và biết tổng diện tích các mặt của lăng trụ bằng 296cm . Tính thể tích khối lăng trụ. A. 128
c
m
2
B. 64
c
m
2
C. 32
c
m
2
D. 60
c
m
2
Đọc tiếp
Cho lăng trụ tứ giác đều có tất cả các cạnh bằng nhau và biết tổng diện tích các mặt của lăng trụ bằng 296cm . Tính thể tích khối lăng trụ.
A. 128 c m 2
B. 64 c m 2
C. 32 c m 2
D. 60 c m 2
Lăng trụ tam giác đều ABC.ABC có góc giữa hai mặt phẳng (ABC) và (ABC) bằng
60
o
, cạnh ABa Thể tích khối đa diện ABCCB bằng A.
3
a
3
4
Đọc tiếp
Lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60 o , cạnh AB=a Thể tích khối đa diện ABCC'B' bằng
A. 3 a 3 4
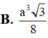
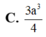
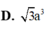
Lăng trụ tam giác đều ABC.ABC có góc giữa hai mặt phẳng (ABC) và (ABC) bằng
60
o
; cạnh ABa Thể tích khối đa diện ABC.CB bằng:
Đọc tiếp
Lăng trụ tam giác đều ABC.A'B'C' có góc giữa hai mặt phẳng (A'BC) và (ABC) bằng 60 o ; cạnh AB=a Thể tích khối đa diện ABC.C'B' bằng:
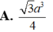
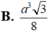
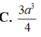
![]()
Cho khối lăng trụ tam giác ABC.ABC có thể tích là V. Gọi I, J lần lượt là trung điểm của hai cạnh AA và BB. Khi đó thể tích của khối đa diện ABCIJC bằng
Đọc tiếp
Cho khối lăng trụ tam giác ABC.A'B'C' có thể tích là V. Gọi I, J lần lượt là trung điểm của hai cạnh AA' và BB'. Khi đó thể tích của khối đa diện ABCIJC' bằng

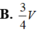
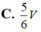
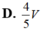
Cho khối lăng trụ BAC.ABC. Mặt phẳng (P) đi qua C và các trung điểm của AA, BB chia khối lăng trụ thành hai khối đa diện có tỉ số thể tích bằng k với k
≤
1
. Tìm k. A.
1
3
B.
2
3
C.
1
D.
1
2
Đọc tiếp
Cho khối lăng trụ BAC.A'B'C'. Mặt phẳng (P) đi qua C' và các trung điểm của AA', BB' chia khối lăng trụ thành hai khối đa diện có tỉ số thể tích bằng k với k ≤ 1 . Tìm k.
A. 1 3
B. 2 3
C. 1
D. 1 2



