Tam thức f(x) = -2x2 + 3x + 5 có hai nghiệm là – 1 và 5/2 ; hệ số a= - 2 < 0.
Do đó, với -1 < x < 5/2 thì f(x) trái dấu với hệ số của x2
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Trong các khoảng nào g(x) = -3x2 + 7x – 4 cùng dấu với hệ số của x2?
Giải bất phương trình -2x + 3 > 0 và biểu diễn trên trục số tập nghiệm của nó
Từ đó hãy chỉ ra các khoảng mà nếu x lấy giá trị trong đó thì nhị thức f(x) = -2x + 3 có giá trị
Trái dấu với hệ số của x;
Cùng dấu với hệ số của x.
Tập nghiệm của pt: x4-8x ²-90Hệ pt: x2+y2+xy7 x2+y2-xy3có nghiệm là.Cho phương trình(x2-3x+3)2-2x2+6x-50 Nếu đặt tx2-3x+3thì phương trình đã cho trở thành phương trình nào Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằngA. -3.B. 2.C. 18.D. 21.
Đọc tiếp
Tập nghiệm của pt: x4-8x ²-9=0
Hệ pt: x2+y2+xy=7
x2+y2-xy=3
có nghiệm là.
Cho phương trình(x2-3x+3)2-2x2+6x-5=0 Nếu đặt t=x2-3x+3
thì phương trình đã cho trở thành phương trình nào
Gọi là tập tất cả các giá trị nguyên của tham số thuộc đoạn −2;6 để phương trình x2+4mx +m2
có hai nghiệm dương phân biệt. Tổng các phần tử trong S bằng
A. -3.
B. 2.
C. 18.
D. 21.
Cho E = {x ≤ Z||x| ≤ 5}, F = {x ∈ N ||x| ≤ 5} và
B = {x ∈ Z|(x – 2)(x + 1)(2x2 – x – 3) = 0}. Chứng minh A ⊂ E và B⊂E
Cho A = {x ∈ R | x2+ x – 12 = 0 và 2x2 – 7x + 3 = 0}
B = {x ∈ Z | 3x2 – 13x + 12 =0 hoặc x2 – 3x = 0}
Đồ thị hàm số
y
f
(
x
)
a
x
2
+
b
x
+
c
được cho trong hình 47. Kí hiệu
Δ
b
2
-
4
a
c
là biệt số của f(x). Trong các khẳng định sau, kh...
Đọc tiếp
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
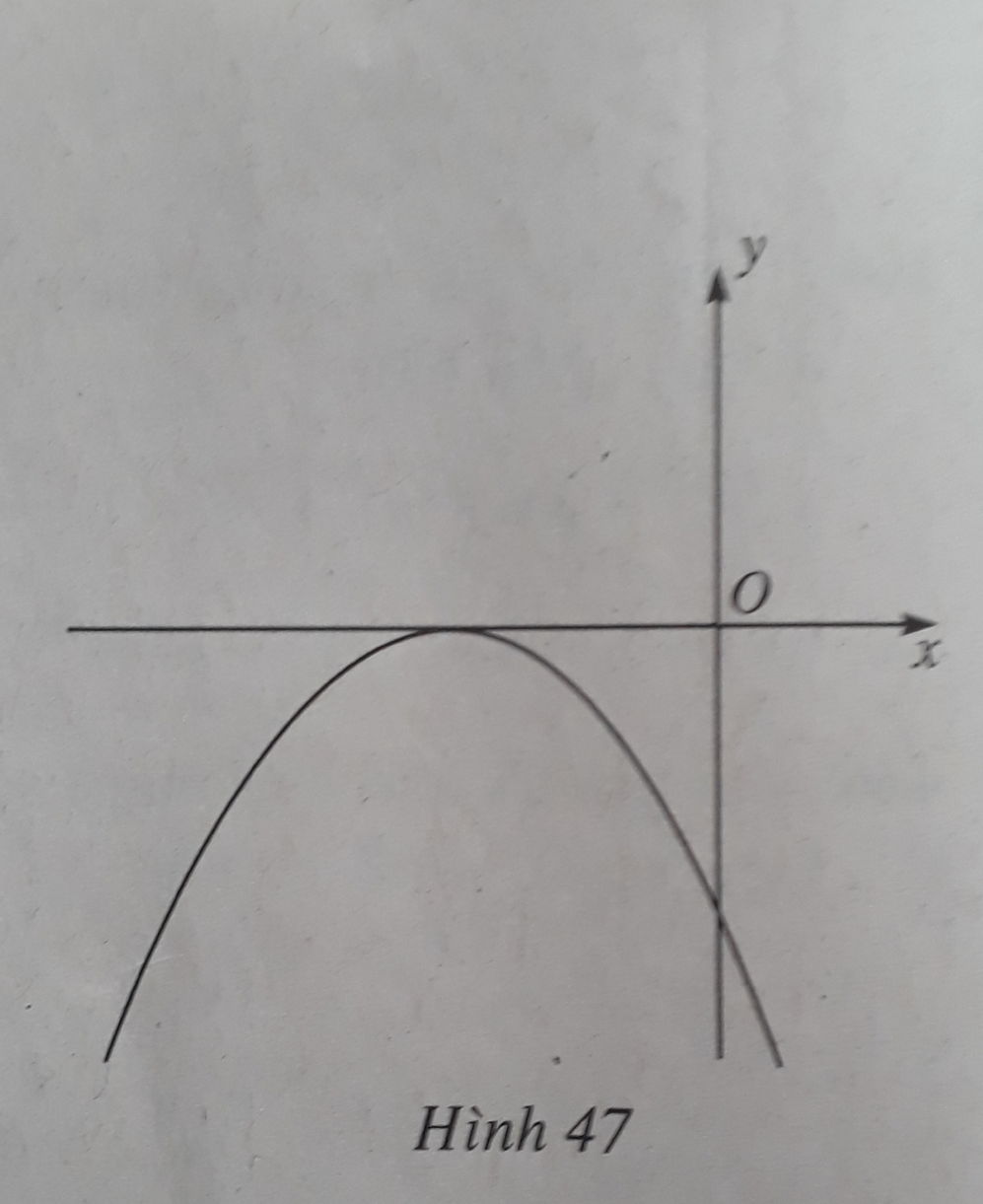
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
Xét tính chẵn lẻ của các hàm số sau:
a) f (x) = -2x3+3x
b) f (x) = x2 + x
c) f (x) =\(\sqrt{6-3x}-\sqrt{6+3x}\)
d) f (x)= \(\dfrac{\sqrt{x+5}-\sqrt{5-x}}{4-x^2}\)
Mn giúp e bài này với ạ.E đang cần gấp ạ.
Tìm các giá trị của tham số m để các phương trình sau có hai nghiệm phân biệt trái dấu
x
2
-
(
m
3
+
m
-
2
)
x
+
m
2
+
m
-
5
0
Đọc tiếp
Tìm các giá trị của tham số m để các phương trình sau có hai nghiệm phân biệt trái dấu
x 2 - ( m 3 + m - 2 ) x + m 2 + m - 5 = 0
Cho hàm số F(x) = (m + 1)x2 - 2mx + m - 2 (m là tham số). a) Tìm m để phương trình f(x) = 0 có hai nghiệm trái dấu? b) Tìm m để bất phương trình f(x) < 0 có một nghiệm đúng với mọi x.
Xét tính đồng biến, nghịch biến của hàm số f(x) x − 3x + 5 trên khoảng (−
∞
; −5) và trên khoảng (−5; +
∞
). Khẳng định nào sau đây đúng? A. Hàm số nghịch biến trên (−
∞
; −5), đồng biến trên (−5; +
∞
). B. Hàm số đồng biến trên (−
∞
; −5), nghịch biến trên (−5; +
∞
). C. Hàm số nghịch biến trên các khoảng (−
∞
; −5) và (−5; +
∞...
Đọc tiếp
Xét tính đồng biến, nghịch biến của hàm số f(x) = x − 3x + 5 trên khoảng (− ∞ ; −5) và trên khoảng (−5; + ∞ ). Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên (− ∞ ; −5), đồng biến trên (−5; + ∞ ).
B. Hàm số đồng biến trên (− ∞ ; −5), nghịch biến trên (−5; + ∞ ).
C. Hàm số nghịch biến trên các khoảng (− ∞ ; −5) và (−5; + ∞ ).
D. Hàm số đồng biến trên các khoảng (− ∞ ; −5) và (−5; + ∞ )