Các câu hỏi tương tự
Trên trục tọa độ
O
;
i
→
cho 2 điểm A ; B có tọa độ lần lượt 3 và – 5.Tọa độ trung điểm I của AB là : A. 2 B. 4 C. -1 D. -2
Đọc tiếp
Trên trục tọa độ O ; i → cho 2 điểm A ; B có tọa độ lần lượt 3 và – 5.Tọa độ trung điểm I của AB là :
A. 2
B. 4
C. -1
D. -2
Trên trục
O
;
i
→
, cho ba điểm A; B; C lần lượt có tọa độ là -5; 2; 4. Tìm tọa độ điểm M thỏa mãn
2
M
A
→
+
4
M
B
→
+
3
M...
Đọc tiếp
Trên trục O ; i → , cho ba điểm A; B; C lần lượt có tọa độ là -5; 2; 4. Tìm tọa độ điểm M thỏa mãn 2 M A → + 4 M B → + 3 M C → = 0 →
A. 10/3
B. -10/3
C. 10/9
D. 9/10
Trên trục
O
;
i
→
cho 3 điểm A; B; C có tọa độ lần lượt là a; b;c . Tìm điểm I sao cho
I
A
→
+
I
B
→
+
I
C
→...
Đọc tiếp
Trên trục O ; i → cho 3 điểm A; B; C có tọa độ lần lượt là a; b;c . Tìm điểm I sao cho I A → + I B → + I C → = 0 →
A. 
B. 
C. 
D. 
Trên trục (O, e→) cho các điểm A, B, M, N có tọa độ lần lượt là -1, 2, 3, -2a) Hãy vẽ trục và biểu diễn các điểm đã cho trên trục;b) Tính độ dài đại số của . Từ đó suy ra hai vec tơ ngược hướng.
Đọc tiếp
Trên trục (O, e→) cho các điểm A, B, M, N có tọa độ lần lượt là -1, 2, 3, -2
a) Hãy vẽ trục và biểu diễn các điểm đã cho trên trục;
b) Tính độ dài đại số của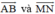 
. Từ đó suy ra hai vec tơ 
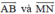ngược hướng.
Cho 3 điểm A(3;-5) B(-2;-2) C(4;1)
a) Tìm tọa độ vecto BC, vecto AC, vecto BA
b) Chứng minh rằng ba điểm A,B,C không thẳng hàng
c) Tìm tọa đọ trung điểm I của AC; J của AB
d) Tìm tọa độ trọng tâm G của tam giác ABC
e) Tìm tọa độ điểm H sao cho A là trọng tâm tam giác HBC
g) Tìm tọa độ điểm D sao cho ABCD là hình bình hành
Cho tam giác ABC có trọng tâm là gốc tọa độ O, hai đỉnh A và B có tọa độ là A(-2;2), B(3;5).Tọa độ trung điểm của OC là
A. (-3/2;-5/2) B. (1/2;-1) C. (-1/2;-7/2) D. (1;7)
28 tháng 12 2021 lúc 8:01
Câu 1: Trong hệ trục (O,overrightarrow{i},overrightarrow{j}), tọa độ overrightarrow{i}-overrightarrow{j}làCâu 2:Cho overrightarrow{a}(3;-4), overrightarrow{b}(-1;2). Tọa độ vecto overrightarrow{a}+2overrightarrow{b}là
Đọc tiếp
Câu 1: Trong hệ trục (O,\(\overrightarrow{i}\),\(\overrightarrow{j}\)), tọa độ \(\overrightarrow{i}\)-\(\overrightarrow{j}\)là
Câu 2:Cho \(\overrightarrow{a}\)(3;-4), \(\overrightarrow{b}\)(-1;2). Tọa độ vecto \(\overrightarrow{a}\)+2\(\overrightarrow{b}\)là
trong mặt phẳng tọa độ oxy, cho 3 điểm A (3;3) B (4;-2) C(-1;-1)
1. tính vecto AB và vecto BC từ đó suy ra A,B, C là ba đỉnh của một tam giác
2. Tìm tọa độ điểm M thỏa mãn vecto MA + 4MB - MC = 0
3. Cho hình bình hành ABCD. Gọi I là trung điểm cạnh bC và E là điểm xác định bởi vecto AE = 2/3AC. CMR: vecto DI = AB - 1/2AD và 3 điểm D, E, I thẳng hàng
Cho hàm số y = f(x) = mx + 2m − 3 có đồ thị (d). gọi A, B là hai điểm thuộc đồ thị
và có hoành độ lần lượt là −1 và 2.
1 Xác định tọa độ hai điểm A và B.
2 Tìm m để cả hai điểm A và B cùng nằm phía trên trục hoành.
3 Tìm điều kiện của m để f(x) > 0, ∀x ∈ [−1; 2]