Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, Cho tam giác ABC biết A(–2 ; 2), B(2 ; – 1), C(5 ; 3 ) và điểm E(–1; 0 ). a) Chứng minh rằng tam giác ABC cân.Tính diện tích tam giác ABC. b) Tìm tọa độ các điểm M(m; 2m-5) sao cho MO=√5AE5AE ( biết O là gốc tọa độ và m lớn hơn 0 ).
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD A. B. C. D.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho A(3; -1) ; B( -1; 2) và I( 1; -1) . Xác định tọa độ các điểm C; D sao cho tứ giác ABCD là hình bình hành biết I là trọng tâm tam giác ABC. Tìm tọa tâm O của hình bình hành ABCD
A. 
B. 
C. 
D. 
Trong mặt phẳng tọa độ Oxy, Cho tam giác ABC biết A(–2 ; 2), B(2 ; – 1), C(5 ; 3 ) và điểm E(–1; 0 ). a) Chứng minh rằng tam giác ABC cân.Tính diện tích tam giác ABC. b) Tìm tọa độ các điểm M(m; 2m-5) sao cho MO=\(\sqrt{5}AE\) ( biết O là gốc tọa độ và m lớn hơn 0 ).
trong mặt phẳng tọa độ oxy, cho 3 điểm A (3;3) B (4;-2) C(-1;-1)
1. tính vecto AB và vecto BC từ đó suy ra A,B, C là ba đỉnh của một tam giác
2. Tìm tọa độ điểm M thỏa mãn vecto MA + 4MB - MC = 0
3. Cho hình bình hành ABCD. Gọi I là trung điểm cạnh bC và E là điểm xác định bởi vecto AE = 2/3AC. CMR: vecto DI = AB - 1/2AD và 3 điểm D, E, I thẳng hàng
Trong mặt phẳng Oxy, cho A( -2; 0) ; B( 5; -4) ; C( -5; 1). Tọa độ điểm D để tứ giác ABCD là hình bình hành là:
A. D( -8; 5).
B. D( 5; 8).
C. D( 8; 5).
D. D( 8; -5).
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ; B( 4; 0) ; C(2; -5). Tọa độ điểm M thỏa mãn
M
A
→
+
M
B
→
-
3
M
C
→
0
→
là A. M(1; -18). B. M(1 ;18). C. M(18; -1). D. M(-18; -1).
Đọc tiếp
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ; B( 4; 0) ; C(2; -5). Tọa độ điểm M thỏa mãn M A → + M B → - 3 M C → = 0 → là
A. M(1; -18).
B. M(1 ;18).
C. M(18; -1).
D. M(-18; -1).
Trong mặt phẳng tọa độ Oxy, cho các điểm M(0,4) và P(9, -3) .Tọa độ điểm N đối xứng với điểm M qua điểm P là : A. N(18,10) B. N(18, -10) C. N(9/2 ; 1/2) D. N(9; -7)
Trong mặt phẳng Oxy, cho các điểm A(-3; 3) ; B(1; 4) ; C( 2; -5). Tọa độ điểm M thỏa mãn
2
M
A
→
-
B
C
→
4
C
M
→
là: A. B. C. D.
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm A(-3; 3) ; B(1; 4) ; C( 2; -5). Tọa độ điểm M thỏa mãn 2 M A → - B C → = 4 C M → là:
A. 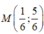
B. ![]()
C. 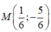
D. 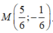
Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có AB :2x -y + 1 = 0, AC : x -y + 1 = 0 và M là trung điểm của CD thuộc đường thẳng 2x + y + 1 = 0 . Tìm tọa độ các đỉnh A, B, C, D