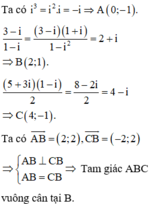Các câu hỏi tương tự
Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức
i
3
,
3
−
i
1
−
i
,
5
+
3
i
1
−...
Đọc tiếp
Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức i 3 , 3 − i 1 − i , 5 + 3 i 1 − i 2 . Khi đó tam giác ABC.
A. vuông cân tại B
B. đều
C. vuông cân tại A
D. vuông cân tại C
Trên mặt phẳng tọa độ cho các điểm
A
,
B
,
C
lần lượt là điểm biểu diễn các số phức
−
1
+
3
i
1
−
i
;
5
i
1
+
2
i
;...
Đọc tiếp
Trên mặt phẳng tọa độ cho các điểm A , B , C lần lượt là điểm biểu diễn các số phức − 1 + 3 i 1 − i ; 5 i 1 + 2 i ; 3 i . Khi đó tam giác ABC:
A. Tam giác đều
B. Vuông cân tại C
C. Vuông tại C
D. Vuông tại A
Trong mặt phẳng tọa độ cho các điểm A, B, C lần lượt là điểm biểu diễn các số phức
-
1
+
3
i
1
-
i
;
5
i
1
+
2
i
;
3
i
. Khi đó tam giác ABC: A. Vuông tại A....
Đọc tiếp
Trong mặt phẳng tọa độ cho các điểm A, B, C lần lượt là điểm biểu diễn các số phức - 1 + 3 i 1 - i ; 5 i 1 + 2 i ; 3 i . Khi đó tam giác ABC:
A. Vuông tại A.
B. Vuông cân tại C.
C. Tam giác đều
D. Vuông tại C.
Trong mặt phẳng phức, cho ba điểm A, B, C lần lượt biểu diễn cho ba số phức
z
1
1
+
i
,
z
2
1
+
i
2
v
à
z
3
a
-
i
a
∈...
Đọc tiếp
Trong mặt phẳng phức, cho ba điểm A, B, C lần lượt biểu diễn cho ba số phức z 1 = 1 + i , z 2 = 1 + i 2 v à z 3 = a - i a ∈ ℝ . Để tam giác ABC vuông tại A thì a bằng
A. -3
B. -2
C. 3
D. -4
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức
z
1
-
3
i
;
z
2
2
-
2
i
;
z
3
5
-
i
. Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là A. z-1-i B. z-1-2i C. z1-2i D. z2-i
Đọc tiếp
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức z 1 = - 3 i ; z 2 = 2 - 2 i ; z 3 = 5 - i . Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là
A. z=-1-i
B. z=-1-2i
C. z=1-2i
D. z=2-i
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức
z
1
-
3
i
;
z
2
2
-
2
i
;
z
3
-
5
-
i
. Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là A.
z...
Đọc tiếp
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức z 1 = - 3 i ; z 2 = 2 - 2 i ; z 3 = - 5 - i . Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là
A. z = - 1 - i
B. z = - 1 - 2 i
C. z = 1 - 2 i
D. z = 2 - i
Trong mặt phẳng (Oxy) cho các điểm A,B,C tương ứng biểu diễn cho các số phức
z
1
1
+
i
;
z
2
1
+
i
2
;
z
3
m
-
i
(với
m
∈
R
). Tìm m để
∆...
Đọc tiếp
Trong mặt phẳng (Oxy) cho các điểm A,B,C tương ứng biểu diễn cho các số phức z 1 = 1 + i ; z 2 = 1 + i 2 ; z 3 = m - i (với m ∈ R ). Tìm m để ∆ A B C vuông tại B.
A. -3
B. -2
C. 3
D. 4
Trong mặt phẳng tọa độ phức Oxy, cho A,B,C là các điểm tương ứng biểu diễn các số phức
z
1
i
,
z
2
−
1
+
2
i
;
z
3
2
. Tọa độ trọng tâm tam giác ABC là A.
1
3
;
0...
Đọc tiếp
Trong mặt phẳng tọa độ phức Oxy, cho A,B,C là các điểm tương ứng biểu diễn các số phức z 1 = i , z 2 = − 1 + 2 i ; z 3 = 2 . Tọa độ trọng tâm tam giác ABC là
A. 1 3 ; 0 .
B. - 1 3 ; 1 .
C. 1 2 ; 3 2 .
D. 1 3 ; 1 .
Trong mặt phẳng tọa độ Oxy, cho ba điểm M, N, P là điểm biểu diễn của 3 số phức:
z
1
8
+
i
;
z
2
1
+
4
i
;
z
3
5
+
x
i
.Tìm x để tam giác MNP vuông tại P A. 1 và 2 B. 0 và 7 C. -1 và -7 D. 3 và 5
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho ba điểm M, N, P là điểm biểu diễn của 3 số phức: z 1 = 8 + i ; z 2 = 1 + 4 i ; z 3 = 5 + x i .Tìm x để tam giác MNP vuông tại P
A. 1 và 2
B. 0 và 7
C. -1 và -7
D. 3 và 5