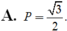\(sin^2\alpha+cos^2\alpha=1\)
=>\(cos^2\alpha=1-\left(\dfrac{1}{5}\right)^2=1-\dfrac{1}{25}=\dfrac{24}{25}\)
=>\(\left[{}\begin{matrix}cos\alpha=\sqrt{\dfrac{24}{25}}=\dfrac{2\sqrt{6}}{5}\\cos\alpha=-\dfrac{2\sqrt{6}}{5}\end{matrix}\right.\)
\(A=sin2a-4\cdot cos2a+1\)
\(=2\cdot sina\cdot cosa-4\cdot\left(1-2\cdot sin^2a\right)+1\)
\(=\dfrac{2}{5}\cdot cosa-4\cdot\left(1-2\cdot\dfrac{1}{25}\right)+1\)
\(=\dfrac{2}{5}\cdot cosa-4\cdot\left(1-\dfrac{2}{25}\right)+1\)
\(=\dfrac{2}{5}\cdot cosa-4\cdot\dfrac{23}{25}+1=\dfrac{2}{5}\cdot cosa-\dfrac{68}{25}\)
TH1: \(cos\alpha=\dfrac{2\sqrt{6}}{5}\)
=>\(A=\dfrac{2}{5}\cdot\dfrac{2\sqrt{6}}{5}-\dfrac{68}{25}=\dfrac{4\sqrt{6}-68}{25}\)
TH2: \(cos\alpha=-\dfrac{2\sqrt{6}}{5}\)
\(A=\dfrac{2}{5}\cdot\dfrac{-2\sqrt{6}}{5}-\dfrac{68}{25}=\dfrac{-4\sqrt{6}-68}{25}\)