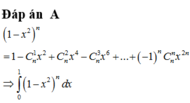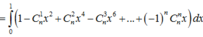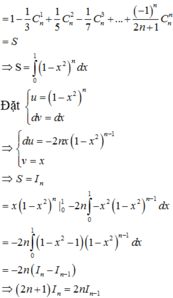Các câu hỏi tương tự
Xét tính tăng - giảm của dãy số (un) với
a) un=\(\dfrac{3^n}{2^{n+1}}\)
b) un=\(\dfrac{3^n}{n^2}\)
c) un=\(\sqrt{n}-\sqrt{n-1}\)
1) Tính \(S=-1+\dfrac{1}{10}-\dfrac{1}{10^2}+...+\dfrac{\left(-1\right)^n}{10^{n-1}}\)
2) Tính \(S=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{n-1}}\)
Giup mình với ạ! Mình cảm ơn nhiều ạ
Tính tổng S= (3+1/3)^2 +(3^2 +1/3^2)^2 +....+( 3^n +1/3^n)^2
1) tính \(\lim\limits_{n\rightarrow\infty}\dfrac{3n^5+3n^3-1}{n^3-2n}\)
2) tính \(\lim\limits_{n\rightarrow\infty}\dfrac{3n^7+3n^5-n}{3n^2-2n}\)
Cho dãy số left(a_nright) xác định bởi công thức:hept{begin{cases}a_11;a_22;na_{n+2}left(3n+2right)a_{n+1}-2left(n+1right)a_n;n1;2;3...end{cases}}a) Tìm công thức số hạng tổng quát của dãy left(a_nright)b)Chứng minh sqrt{a_1-1}+sqrt{a_2-1}+...+sqrt{a_n-1}gefrac{nleft(n+1right)}{2};forall ninℕ^∗c) Tính limleft(frac{a_1}{3}+frac{a_2}{3^2}+...+frac{a_n}{3^n}right)
Đọc tiếp
Cho dãy số \(\left(a_n\right)\) xác định bởi công thức:
\(\hept{\begin{cases}a_1=1;a_2=2;\\na_{n+2}=\left(3n+2\right)a_{n+1}-2\left(n+1\right)a_n;n=1;2;3...\end{cases}}\)
a) Tìm công thức số hạng tổng quát của dãy \(\left(a_n\right)\)
b)Chứng minh \(\sqrt{a_1-1}+\sqrt{a_2-1}+...+\sqrt{a_n-1}\ge\frac{n\left(n+1\right)}{2};\forall n\inℕ^∗\)
c) Tính \(lim\left(\frac{a_1}{3}+\frac{a_2}{3^2}+...+\frac{a_n}{3^n}\right)\)
1) tính \(\lim\limits_{n\rightarrow\infty}\dfrac{-6n^5+3n^3-1}{n^4-8n}\)
2) tính \(\lim\limits_{n\rightarrow\infty}\dfrac{-5n^7+8n^5-n}{5n^6-2n}\)
xét tính tăng, giảm của các dãy số sau
a) \(u_n=2n-1\)
b) \(u_n=3-2n\)
c) \(u_n=\dfrac{n+2}{n}\)
d) \(u_n=\dfrac{2}{n}\)
e) \(u_n=3^n\)
xét tính tăng, giảm của các dãy số sau
a) \(u_n=2-3n\)
b) \(u_n=\dfrac{n+1}{n}\)
c) \(u_n=\dfrac{1}{n+1}\)
d) \(u_n=2^n\)
Tính tổng
S
-
C
n
1
2
.
3
+
2
C
n
2
3
.
4
-
3
C
n...
Đọc tiếp
Tính tổng S = - C n 1 2 . 3 + 2 C n 2 3 . 4 - 3 C n 3 4 . 5 + . . . + ( - 1 ) n n C n n ( n + 1 ) ( n + 2 )

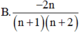
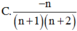
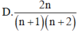
1) Tính giới hạn \(K=\lim\limits_{n\rightarrow\infty}\left(\dfrac{3.2^n-3^n}{2^{n+1}+3^{n+1}}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\dfrac{3^n-4^{n+1}}{3^{n+2}+4^n}\right)\)