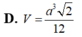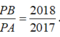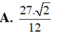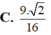Question

Tính thể tích khối tứ diện đều S.ABC có cạnh bằng a

Answer 1

Lời giải:

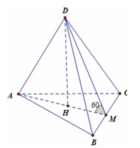
Kẻ $SH\perp $(ABC)$ thì $H$ là tâm tam giác đều $ABC$

Có:

$AH=\frac{2}{3}d(A,BC)=\frac{2}{3}\sqrt{a^2-(\frac{a}{2})^2}=\frac{2}{3}.\frac{\sqrt{3}a}{2}=\frac{\sqrt{3}a}{3}$

$SH=\sqrt{SA^2-AH^2}=\sqrt{a^2-(\frac{\sqrt{3}a}{3})^2}=\frac{\sqrt{6}a}{3}$

$S_{ABC}=BC.d(A,BC):2=a.\sqrt{a^2-(\frac{a}{2})^2}:2=\frac{\sqrt{3}}{4}a^2$
Thể tích $S.ABC$ là:

$V=\frac{1}{3}SH.S_{ABC}=\frac{1}{3}.\frac{\sqrt{6}}{3}a.\frac{\sqrt{3}}{4}a^2$
$=\frac{\sqrt{2}a^3}{12}$