Đáp án B.
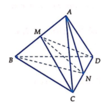
Gọi ABCD là tứ diện đều cạnh a.
Gọi M là trung điểm của AB và N là trung điểm của CD.
Do NA=NB nên tam giác NAB cân ⇒ M N ⊥ A B .
Do MC=MD nên tam giác MCD cân ⇒ M N ⊥ C D .
Suy ra MN là đoạn vuông góc chung của AB và CD.
Tam giác BMN vuông tại M
⇒ M N = B N 2 - B M 2 = a 3 2 2 - a 2 2 = 2 a 2 4 = a 2 2 .
Vậy d ( A B , C D ) = M N = a 2 2 . Vậy ta chọn B.
Tính khoảng cách giữa hai cạnh đối của một tứ diện đều cạnh a.
A. 3 a 2
B. a 2 2
C. a 3 2
D. a 2
Cho tứ diện đều ABCD cạnh a, tính khoảng cách giữa hai đường thẳng AB và CD
A. a 2 2
B. a 3 2
C. a 3 3
D. a
Cho tứ diện đều ABCD có cạnh a. Tính khoảng cách giữa hai đường thẳng AB và CD.
A. a 2
B. a 2 2
C. a 2
D. a
Tứ diện đều ABCD có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng AB và CD
A. a 3
B. a 3 2
C. a 2 2
D. a
Cho tứ diện đều ABCD cạnh bằng a. Khoảng cách d giữa hai đường thẳng AD và BC là:
A. d = a 3 2
B. d = a 2 2
C. d = a 2 3
D. d = a 3 3
Cho tứ diện đều ABCD cạnh bằng a . Khoảng cách d giữa hai đường thẳng AD và BC là:
A. d = a 3 2
B. d = a 2 2
C. d = a 2 3
D. d = a 3 3
Cho hình tứ diện đều ABCD cạnh bằng a, gọi d là khoảng cách giữa hai đường thẳng AB và CD .Tìm d
A. d(AB;CD)=a
B. d(AB;CD)=a/3
C. d(AB;CD)=a/2
D. d A B ; C D = a 2 2
Cho hình chóp đều S.ABCD có cạnh đáy bằng 2 a , cạnh bên bằng 3 a . Gọi M là trung điểm CD. Khoảng cách giữa hai đường thẳng AC và SM bằng
A. 2 a 3
B. 2 2 a 3
C. 2 a 3
D. a.
Cho tứ diện đều A B C D cạnh bằng a . Khoảng cách giữa hai đường thẳng A B và C D bằng
A. 3 a 2 .
B. a .
C. a 3 2 .
D. a 2 2 .
