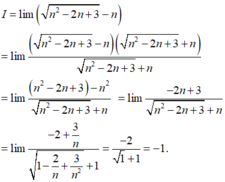Các câu hỏi tương tự
1) tính giới hạn \(\lim\limits_{n\rightarrow\infty}\sqrt{n^2-1}+3n\)
2) tính giới hạn I = \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{4n^2+5}+n\right)\)
1) Tính \(I=\lim\limits_{n\rightarrow\infty}\left(\sqrt{n^2+2}-\sqrt{n^2-1}\right)\)
2) Tính giới hạn \(\lim\limits_{n\rightarrow\infty}\left(\sqrt{n^2+2n+2}+n\right)\)
Tính giới hạn I lim
2
n
(
3
-
n
)
+
1
1
+
3
+
5
+
.
.
+
(
2
n
-
1...
Đọc tiếp
Tính giới hạn I = lim 2 n ( 3 - n ) + 1 1 + 3 + 5 + . . + ( 2 n - 1 ) .
A. I = 2
B. I = 1
C. I = -2
D. I = -3
Bài 1. (1,0 điểm) Tính giới hạn: $\lim(\sqrt{{{n}^{2}}+1}-n)$.
Tính giới hạn I = l i m n 2 - 2 n + 3 - n
A. I = -1
B. I= 1
C. I = 0
D. I = + ∞
Tính giới hạn I = lim ( n 2 - 4 n + 8 - n )
A. I = + ∞
B. I = 0
C. I = -2
D. I = 1
Tính giới hạn I
l
i
m
2
n
+
1
2
+
n
-
n
2
A. I
-
∞
B. I -2 C. I 1 D. I 0
Đọc tiếp
Tính giới hạn I = l i m 2 n + 1 2 + n - n 2
A. I = - ∞
B. I = -2
C. I = 1
D. I = 0
Trong không gian, cho bốn mặt cầu có bán kính lần lượt là 2, 3, 3, 2 (đơn vị độ dài) tiếp xúc ngoài với nhau. Mặt cầu nhỏ nhất tiếp xúc ngoài với cả bốn mặt cầu nói trên có bán kính bằng?
Tính giới hạn:
I
lim
x
→
0
c
o
s
3
x
-
cos
7
x
x
2
A. 40...
Đọc tiếp
Tính giới hạn: I = lim x → 0 c o s 3 x - cos 7 x x 2
A. 40
B. 0
C. -4
D. 20