Các câu hỏi tương tự
Cho số phức zx+yi với x, y là các số thực không âm thỏa mãn
z
-
3
z
-
1
+
2
i
1
và biểu thức
P
z
2
-...
Đọc tiếp
Cho số phức z=x+yi với x, y là các số thực không âm thỏa mãn z - 3 z - 1 + 2 i = 1 và biểu thức P = z 2 - z - 2 + i ( z 2 - z - 2 ) z ( 1 - i ) + z ¯ ( 1 + i ) . Giá trị lớn nhất và giá trị nhỏ nhất của P lần lượt là:
A. 0 và -1
B. 3 và -1
C. 3 và 0
D. 2 và 0
Cho z là số phức thay đổi thỏa mãn
(
1
+
i
)
z
+
2
-
i
4
và M(x,y) là điểm biểu diễn cho z trong mặt phẳng phức. Tìm giá trị lớn nhất của biểu thức
T
x
+
y
+...
Đọc tiếp
Cho z là số phức thay đổi thỏa mãn ( 1 + i ) z + 2 - i = 4 và M(x,y) là điểm biểu diễn cho z trong mặt phẳng phức. Tìm giá trị lớn nhất của biểu thức T = x + y + 3
A. T = 4 + 2 2
B. 8
C. 4
D. 4 2
Biết
∫
x
+
1
(
x
-
1
)
(
x
-
2
)
d
x
a
ln
x
-
1
+
b
ln
x
-...
Đọc tiếp
Biết ∫ x + 1 ( x - 1 ) ( x - 2 ) d x = a ln x - 1 + b ln x - 2 + C , ( a , b ∈ ℝ ) . Tính giá trị của biểu thức
A. a+b =1
B. a+b =5
C. a+b =-5
D. a+b =-1
Cho số phức
z
x
+
y
i
với
x
;
y
∈
R
thỏa mãn
z
-
1
-
i
≥
1
và
z
-
3
-
3
i
≤
5
....
Đọc tiếp
Cho số phức z = x + y i với x ; y ∈ R thỏa mãn z - 1 - i ≥ 1 và z - 3 - 3 i ≤ 5 . Gọi m; M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P = x+2y. Tính tỉ số M m
A. 9 4
B. 7 2
C. 5 4
D. 14 5
Tích phân
I
∫
0
1
(
x
-
1
)
2
x
2
+
1
d
x
a
ln
b
+
c
, trong đó a; b; c là số nguyên. Tính giá trị của biểu th...
Đọc tiếp
Tích phân I = ∫ 0 1 ( x - 1 ) 2 x 2 + 1 d x = a ln b + c , trong đó a; b; c là số nguyên. Tính giá trị của biểu thức a+b+c.
![]()
![]()
![]()
![]()
Cho 2 số phức
z
1
,
z
2
thỏa mãn
2
z
1
-
i
...
Đọc tiếp
Cho 2 số phức z 1 , z 2 thỏa mãn 2 z 1 - i = 2 + i z 1 2 z 2 - i = 2 + i z 2 z 1 - z 2 = 1 Tính giá trị của biểu thức P = z 1 + z 2
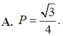
![]()
![]()
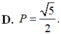
Cho z1, z2 là hai số phức thảo mãn
2
z
−
i
2
+
i
z
, biết
z
1
−
z
2
1
. Tính giá trị của biểu thức
P...
Đọc tiếp
Cho z1, z2 là hai số phức thảo mãn 2 z − i = 2 + i z , biết z 1 − z 2 = 1 . Tính giá trị của biểu thức P = z 1 + z 2
A. P = 3 2
B. P = 2
C. P = 2 2
D. P = 3
Đồ thị hàm số y f(x) đối xứng với đồ thị hàm số
y
log
a
x
(
0
a
≠
1
)
qua điểm I(2; 1). Giá trị của biểu thức
f
(
4
-
a
2019
)
bằng A. 2023 B. -2023 C. 2017 D. -2017
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị hàm số y = log a x ( 0 < a ≠ 1 ) qua điểm I(2; 1). Giá trị của biểu thức f ( 4 - a 2019 ) bằng
A. 2023
B. -2023
C. 2017
D. -2017
Đồ thị hàm số y f(x) đối xứng với đồ thị của hàm số
y
a
x
(
a
0
,
a
≠
1
)
qua điểm I(1;1). Giá trị của biểu thức
2
+
log
a
1
2018
bằng
Đọc tiếp
Đồ thị hàm số y = f(x) đối xứng với đồ thị của hàm số y = a x ( a > 0 , a ≠ 1 ) qua điểm I(1;1). Giá trị của biểu thức 2 + log a 1 2018 bằng
![]()
![]()
![]()
![]()








