Các câu hỏi tương tự
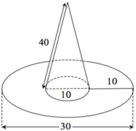
Tính diện tích vải cần có để may một cái mũ có dạng và kích thước (cùng đơn vị đo) được cho bởi hình vẽ bên (không kể riềm, mép) A.
350
π
B.
400
π
C.
450
π
D.
500
π
Đọc tiếp
Tính diện tích vải cần có để may một cái mũ có dạng và kích thước (cùng đơn vị đo) được cho bởi hình vẽ bên (không kể riềm, mép)
A. 350 π
B. 400 π
C. 450 π
D. 500 π
Một cái mũ bằng vải của nhà ảo thuật gia gồm phần dạng hình trụ (có tổng diện tích vải là
S
1
) và phần dạng hình vành khăn (có tổng diện tích vải là
S
2
) với các kích thước như hình vẽ. Tính tổng
r
+
d
sao cho biểu thức
P
3
S
2
−
S
1
đạt giá trị lớn nhất. (Không...
Đọc tiếp
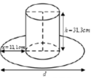
Một cái mũ bằng vải của nhà ảo thuật gia gồm phần dạng hình trụ (có tổng diện tích vải là S 1 ) và phần dạng hình vành khăn (có tổng diện tích vải là S 2 ) với các kích thước như hình vẽ. Tính tổng r + d sao cho biểu thức P = 3 S 2 − S 1 đạt giá trị lớn nhất. (Không kể viền, mép, phần thừa).
A. 28,6
B. 26,2
C. 30,8
D. 28,2
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao
h
1
,
5
m
gồm:- Phần dưới có dạng hình trụ bán kính đáy
R
1
m
và có chiều cao bằng
1
3
h
;- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng
1
2
R
ở phía trên (ngườ...
Đọc tiếp
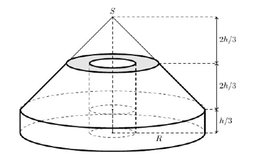
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao h = 1 , 5 m gồm:
- Phần dưới có dạng hình trụ bán kính đáy R = 1 m và có chiều cao bằng 1 3 h ;
- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng 1 2 R ở phía trên (người ta thường gọi hình đó là hình nón cụt);
- Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng 1 4 R (tham khảo hình vẽ bên dưới).
Thể tích của khối bê tông (làm tròn đến chữ số thập phân thứ ba) bằng
A. 2 , 815 m 3
B. 2 , 814 m 3
C. 3 , 403 m 3
D. 3 , 109 m 3
Cho khối hình học có dạng hình vẽ dưới đây, các kích thước đã ghi (cùng đơn vị đo). Tính thể tích của các khối đó A.
V
80
3
π
.
B.
V
48
5
π
.
C.
V
64
3
π
.
D.
V
12
π
.
Đọc tiếp
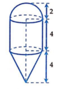
Cho khối hình học có dạng hình vẽ dưới đây, các kích thước đã ghi (cùng đơn vị đo). Tính thể tích của các khối đó
A. V = 80 3 π .
B. V = 48 5 π .
C. V = 64 3 π .
D. V = 12 π .
Lượng nguyên liệu cần dùng để làm ra một chiếc nón lá được ước lượng qua phép tính diện tích xung quanh của mặt nón. Cứ 1kg lá dùng để làm nón có thể làm ra số nón có tổng diện tích xung quanh là
6
,
13
m
2
. Hỏi nếu muốn làm ra 1000 chiếc nón lá giống nhau có đường kính vành nón là 50cm, chiều cao 30cm thì cần khối lượng lá gần nhất với con số nào dưới đây? (coi mỗi chiếc nón là có hình dạng là 1 hình nón). A. 48 B...
Đọc tiếp
Lượng nguyên liệu cần dùng để làm ra một chiếc nón lá được ước lượng qua phép tính diện tích xung quanh của mặt nón. Cứ 1kg lá dùng để làm nón có thể làm ra số nón có tổng diện tích xung quanh là 6 , 13 m 2 . Hỏi nếu muốn làm ra 1000 chiếc nón lá giống nhau có đường kính vành nón là 50cm, chiều cao 30cm thì cần khối lượng lá gần nhất với con số nào dưới đây? (coi mỗi chiếc nón là có hình dạng là 1 hình nón).
A. 48
B. 38
C. 50
D. 76
Một phần dụng cụ gồm một phần có dạng trụ, phần còn lại có dạng nón. một hình trụ, đường kính đáy 1,4m, chiều cao 70cm, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m (Các kích thước cho trên hình 100). Khi đó diện tích mặt ngoài của dụng cụ (Không tính nắp đậy) có giá trị gần nhất với: A. 5,58 B.6,13 C. 4,86 D. 6,36
Đọc tiếp
Một phần dụng cụ gồm một phần có dạng trụ, phần còn lại có dạng nón. một hình trụ, đường kính đáy 1,4m, chiều cao 70cm, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m (Các kích thước cho trên hình 100). Khi đó diện tích mặt ngoài của dụng cụ (Không tính nắp đậy) có giá trị gần nhất với:
A. 5,58
B.6,13
C. 4,86
D. 6,36
Một hộp đựng Chocolate bằng kim loại có hình dạng lúc mở nắp như hình vẽ dưới đây. Một phần tư thể tích phía trên hộp được rải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi
x
x
0
là giá trị làm cho hộp kim loại có thể tích lớn nhất, khi đó thể tích chocolate nguyên chất có giá trị
V
0
bằng A.
V...
Đọc tiếp
Một hộp đựng Chocolate bằng kim loại có hình dạng lúc mở nắp như hình vẽ dưới đây. Một phần tư thể tích phía trên hộp được rải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi x = x 0 là giá trị làm cho hộp kim loại có thể tích lớn nhất, khi đó thể tích chocolate nguyên chất có giá trị V 0 bằng
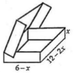
A. V 0 = 64 ( d v t t )
B. V 0 = 64 3 ( d v t t )
C. V 0 = 16 ( d v t t )
D. V 0 = 48 ( d v t t )
Trong một hộp có chứa các tấm bìa dạng hình chữ nhật có kích thước đôi một khác nhau, các cạnh của hình chữ nhật có kích thước là m và n (
m
,
n
∈
N
;
1
≤
m
,
n
≤
20
,
đơn vị là cm). Biết rằng mỗi bộ kích thước ( m,n) đều có tấm bìa tương ứng. Ta gọi một tấm bìa là “tốt” nếu tấm bìa đó có thể được lắp ghép từ các miếng bìa dạng hình chữ L gồm 4 ô vuông, mỗi ô có độ dài cạnh l...
Đọc tiếp
Trong một hộp có chứa các tấm bìa dạng hình chữ nhật có kích thước đôi một khác nhau, các cạnh của hình chữ nhật có kích thước là m và n ( m , n ∈ N ; 1 ≤ m , n ≤ 20 , đơn vị là cm). Biết rằng mỗi bộ kích thước ( m,n) đều có tấm bìa tương ứng. Ta gọi một tấm bìa là “tốt” nếu tấm bìa đó có thể được lắp ghép từ các miếng bìa dạng hình chữ L gồm 4 ô vuông, mỗi ô có độ dài cạnh là 1cm để tạo thành nó (Xem hình vẽ minh họa một tấm bìa “tốt” bên dưới) .
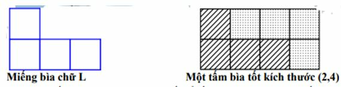
Rút ngẫu nhiên một tấm bìa từ hộp, tính xác suất để tấm bìa vừa rút được là tấm bìa “tốt”
A. 29/95
B. 2/7
C. 29/105
D. 9/35
Một hợp đựng Chocolate bằng kim loại có hình dạng lúc mở nắp . Một phần tư thể tích phía trên của hộp được dải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi x
x
0
là giá trị làm cho hộp kim loại có thể tích lớn nhất, khi đó thể tích chocolate nguyên chất có giá trị là
V
0
. Tìm
V
0
. A. 48 đvtt B. 16...
Đọc tiếp
Một hợp đựng Chocolate bằng kim loại có hình dạng lúc mở nắp . Một phần tư thể tích phía trên của hộp được dải một lớp bơ sữa ngọt, phần còn lại phía dưới chứa đầy chocolate nguyên chất. Với kích thước như hình vẽ, gọi x = x 0 là giá trị làm cho hộp kim loại có thể tích lớn nhất, khi đó thể tích chocolate nguyên chất có giá trị là V 0 . Tìm V 0 .
A. 48 đvtt
B. 16 đvtt
C. 64 đvtt
D. 64 3 đvtt