Các câu hỏi tương tự
Tính diện tích lớn nhất
S
max
của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính
R
6
c
m
nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp. A.
S
max
36
π
c
m
2
B.
S
max
36...
Đọc tiếp
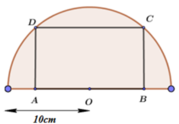
Tính diện tích lớn nhất S max của một hình chữ nhật nội tiếp trong nửa đường tròn bán kính R = 6 c m nếu một cạnh của hình chữ nhật nằm dọc theo đường kính của hình tròn mà hình chữ nhật đó nội tiếp.

A. S max = 36 π c m 2
B. S max = 36 c m 2
C. S max = 96 π c m 2
D. S max = 18 c m 2
Cho nửa đường tròn đường kính AB 2 và hai điểm C, D thay đổi trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng A.
1
2
B.
3
3
4
C. 1 D.
3
3
2
Đọc tiếp
Cho nửa đường tròn đường kính AB = 2 và hai điểm C, D thay đổi trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng
A. 1 2
B. 3 3 4
C. 1
D. 3 3 2
Cho hình vẽ dưới đây trong đó A, B, C, D lần lượt là tâm của bốn đường tròn có bán kính bằng nhau, chúng tạo thành một hình vuông có cạnh là 4. Bốn đường tròn nhỏ bằng nhau và tâm của nó nằm trên các cạnh của hình vuông ABCD và mồi đường tròn này tiếp xúc với hai đường tròn lớn. Tìm diện tích lớn nhất của phần in đậm A. 5.38 B. 7.62 C. 5.98 D. 4.44
Đọc tiếp
Cho hình vẽ dưới đây trong đó A, B, C, D lần lượt là tâm của bốn đường tròn có bán kính bằng nhau, chúng tạo thành một hình vuông có cạnh là 4. Bốn đường tròn nhỏ bằng nhau và tâm của nó nằm trên các cạnh của hình vuông ABCD và mồi đường tròn này tiếp xúc với hai đường tròn lớn. Tìm diện tích lớn nhất của phần in đậm
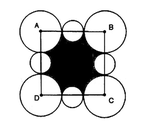
A. 5.38
B. 7.62
C. 5.98
D. 4.44
Một hình nón có chiều cao
S
O
50
c
m
và có bán kính đáy bằng
10
c
m
.
Lấy điểm M thuộc đoạn SO sao cho
O
M
20
c
m
.
Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn
C
. Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi
C...
Đọc tiếp
Một hình nón có chiều cao S O = 50 c m và có bán kính đáy bằng 10 c m . Lấy điểm M thuộc đoạn SO sao cho O M = 20 c m . Một mặt phẳng qua M vuông góc với SO cắt hình nón theo giao tuyến là đường tròn C . Tính diện tích xung quanh của hình nón đỉnh S có đáy là hình tròn xác định bởi C (xem hình vẽ).
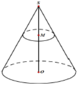
A. 16 π 26 c m 2
B. 26 π 26 c m 2
C. 36 π 26 c m 2
D. 46 π 26 c m 2
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AD8,CD6,AC12. Tính diện tích toàn phần
S
t
p
của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và A′B′C′D′. A.
S
t
p
576
π
B.
S
t
p
10
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AD=8,CD=6,AC'=12. Tính diện tích toàn phần S t p của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và A′B′C′D′.
A. S t p = 576 π
B. S t p = 10 2 11 + 5 π
C. S t p = 26 π
D. S t p = 5 4 11 + 5 π
Cho hình trụ (T) có hai đường tròn đáy O và O. Một hình vuông ABCD nội tiếp trong hình trụ (trong đó các điểm
A
,
B
∈
O
;
C
,
D
∈
O
). Biết hình vuông ABCD có diện tích bằng
400
c
m
2
. Tìm thể tích lớn nhất của khối trụ (T). A.
V...
Đọc tiếp
Cho hình trụ (T) có hai đường tròn đáy O và O'. Một hình vuông ABCD nội tiếp trong hình trụ (trong đó các điểm A , B ∈ O ; C , D ∈ O ' ). Biết hình vuông ABCD có diện tích bằng 400 c m 2 . Tìm thể tích lớn nhất của khối trụ (T).
A. V m a x = 8000 6 3 π
B. V m a x = 8000 3 9 π
C. V m a x = 8000 6 9 π
D. V m a x = 8000 6 12 π
Cho hình lập phương ABCD.A′B′C′D′. Gọi O,O′ lần lượt là tâm của hai hình vuông ABCD và A′B′C′D′. Gọi
V
1
là thể tích của khối trụ tròn xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A′B′C′D′,
V
2
là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A′B′C′D′. Tỷ số thể tích
V
1
V
2...
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′. Gọi O,O′ lần lượt là tâm của hai hình vuông ABCD và A′B′C′D′. Gọi V 1 là thể tích của khối trụ tròn xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A′B′C′D′, V 2 là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A′B′C′D′. Tỷ số thể tích V 1 V 2 là
A. 6
B. 2
C. 8
D. 4
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là A.
S
xq
13
πa
2
4
B.
S
xq...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là
A. S xq = 13 πa 2 4
B. S xq = 37 πa 2 12
C. S xq = 13 πa 2 12
D. S xq = 37 πa 2 4
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết
A
B
4
,
A
D
7
. Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN. A.
104
3
π
B.
116
3
π
C.
44
3
π
D....
Đọc tiếp
Cho hình chữ nhật ABCD và nửa đường tròn đường kính AB như hình vẽ. Gọi M, N lần lượt là trung điểm của AB, CD. Biết A B = 4 , A D = 7 . Tính thể tích V của vật thể tròn xoay khi quay mô hình trên quanh trục MN.
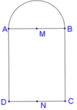
A. 104 3 π
B. 116 3 π
C. 44 3 π
D. 1000 3 π