a) Diện tích hình phẳng giới hạn bởi \(y=2x-5;y=0;x=0;x=2\)
Vì \(2x-5< 0;x\in\left[0;2\right]\)
\(\Rightarrow S=\int\limits^2_0\left(5-2x\right)dx\)
\(\Rightarrow S=\left[5x-x^2\right]^2_0=\left(10-4\right)-\left(0-0\right)=6\left(đvdt\right)\)
b) Diện tích hình phẳng giới hạn bởi \(y=-x-4;Ox\left(y=0;x=-1;x=-9\right)\)
Vì \(\left\{{}\begin{matrix}-x-4>0;x\in[-9;-4)\\-x-4< 0;x\in(-4;-1]\end{matrix}\right.\)
\(S=\int\limits^{-1}_{-9}\left|-x-4-0\right|dx=\int\limits^{-4}_{-9}\left(-x-4\right)dx+\int\limits^{-1}_{-4}\left(x+4\right)dx\)
\(\Rightarrow S=\left[-\dfrac{x^2}{2}-4x\right]^{-4}_{-9}+\left[\dfrac{x^2}{2}+4x\right]^{-1}_{-4}\)
\(\Rightarrow S=\left(-\dfrac{16}{2}+16\right)-\left(-\dfrac{81}{2}+36\right)+\left(\dfrac{1}{2}-4\right)-\left(\dfrac{16}{2}-16\right)=17\left(đvdt\right)\)





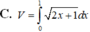
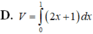
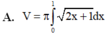
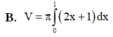
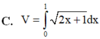
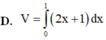
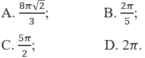
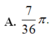
 .
. .
.