Phương pháp:
Sử dụng công thức tính đạo hàm của hàm mũ:
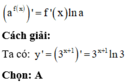
Phương pháp:
Sử dụng công thức tính đạo hàm của hàm mũ:
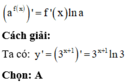
Tính đạo hàm của hàm số y = ln ( x + x 2 + 1 )
A. y ' = 1 x + x 2 + 1
B. y ' = 1 x 2 + 1
C. y ' = x + x 2 + 1
d. y ' = x x + x 2 + 1
Tính đạo hàm của hàm số y = ln ( x 2 + 1 - x )
A. y ' = - 1 x 2 + 1 - x
B. y ' = - 1 x 2 + 1
C. y ' = 1 x 2 + 1
D. y ' = x x 2 + 1
Đạo hàm của hàm số y = x + 2 x - 1 ln ( x + 2 ) là
A. y ' = 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
B. y ' = x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
C. y ' = 2 x log ( 2 x - 1 ) + 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
D. y ' = - 2 x log ( 2 x - 1 ) - 2 x 2 ( 2 x - 1 ) ln 10 log 2 ( 2 x - 1 )
tính đạo hàm sau
\(y=ln\left(\frac{1-x^2}{1+x^2}\right)\)
Cho hàm số f(x)=ln2018-ln(x+1 / x).Tính S=f’(1)+f’(2)+f’(3)+…+f’(2017)
A. 4035 2018
B. 2017
C. 2016 2017
D. 2017 2018
Tìm tập xác định của hàm số y = ln ( 1 - x + 1 ) là
A . [ - 1 ; 0 ]
B . ( - 1 ; + ∞ )
C . ( - 1 ; 0 )
D . ( - 1 ; 0 )
Cho hàm số y = f(x). Hàm số y = f ' x có đồ thị như hình bên. Biết f(-1) = 1, f - 1 e = 2 . Bất phương trình f(x) < ln(-x) + m đúng với mọi x ∈ - 1 ; - 1 e khi và chỉ khi
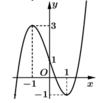
A. m > 2
B. m ≥ 2
C. m > 3
D. m ≥ 3
Phương trình tiếp tuyến của đồ thị hàm số y = ln(x2 – x +1) tại điểm có hoành độ x=1
A. y = x – 1
B. y = x + 1
C. y = x – 1 + ln3
D. y = x + 1 – ln3
Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .
A. S = - 3 ; 3
B. S = 3
C. S = ∅
D. S = - 3
Cho bài toán: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 x 4 − 4 x 2 + 3 . Dưới đây là lời giải của học sinh:
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Tính y 0 = 3 ; y − 1 = y 1 = 1 . Vậy giá trị lớn nhất của hàm số là 3, và giá trị nhỏ nhất là 1.
Lời giải trên đúng hay sai? Nếu sai thì giải sai từ bước mấy?
A. Bước 2
B. Lời giải đúng
C. Bước 3
D. Bước 1