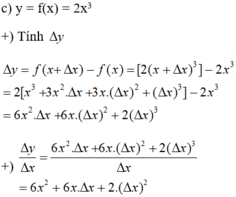Các câu hỏi tương tự
Cho hàm số có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y -x + 2 và tiếp xúc với (H) thì phương trình của Δ là A. y x + 4. D. Không tồn tại.
Đọc tiếp
Cho hàm số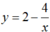 
có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δ là
A. y = x + 4.
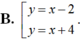
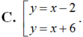
D. Không tồn tại.
21 tháng 2 2022 lúc 21:35
Trong mặt phẳng với hệ tọa độ Oxy. Phép tịnh tiến theo vectơ
biến đường thẳng Δ: x - y -1 = 0 thành đường thẳng Δ' có phương trình là
A.x - y - 1 = 0 .
B. x + y - 1 = 0 .
C. x - y - 2 = 0 .
D. x + y + 2 = 0 .
Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : y = 1 x
Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : y = 2x - 5
Tính Δ y và ∆ y ∆ x của các hàm số sau theo x và Δ x : y = x 2 - 1
cho hàm số y=f(x)=-x3+2x2-x+5 có đồ thị (C). Tìm tham số m để tiếp tuyến Δ của đồ thị (C) tại tiếp điểm A(2;3) song song với đường thẳng (d): (m2-3m-5)x-y-2m+19=0
2. Số gia của hàm số y = 2x^2 -3x +1 theo x và denta x là? 3. Số gia của hàm số y = ✓2x^2 +1 theo x và denta x là?
tính đạo hàm của các hàm số sau
a) \(y=\dfrac{x^2+3x-1}{x+2}\)
b) \(y=\dfrac{2x^2-x}{x^2+1}\)
c) \(y=\dfrac{3-2x}{x-1}+\sqrt{2x-3}\)
Tính các đạo hàm của hàm số sau:
a) \(y=\sqrt{x}\left(x+3\right)\)
b) \(y=\sqrt{2x^2-6x-9}\)
c) \(y=\left(\sqrt{x^2+1}+x\right)^{10}\)