Các câu hỏi tương tự
Tính các tích phân sau: 1) 2 ln e e x dx ; 2) 1 3 2 0 4 x dx x ; 3) /2 /4 1 tan dx x ; 4) 1 0 x e dx ; 5) 2 1 x xe dx ; 6) 0 1 3 4 dx x ; 7) 2 1 4 4 5 dx x x ; 8) 2 0 ln 1 x dx x (HD: 1 u x ) ĐS: 1) 2 e ; 2) 16 7 5 3 ; 3) ln 2 ; 4) 2
Tính diện tích hình phẳng giới hạn bởi các đường sau:a) y 2x –
x
2
, x + y 2 ;b) y
x
3
– 12x, y
x
2
c) x + y 1, x + y -1, x – y 1, x – y -1;d) e) y
x
3
– 1 và tiếp tuyến với y
x
3
– 1 tại điểm (-1; -2).
Đọc tiếp
Tính diện tích hình phẳng giới hạn bởi các đường sau:
a) y = 2x – x 2 , x + y = 2 ;
b) y = x 3 – 12x, y = x 2
c) x + y = 1, x + y = -1, x – y = 1, x – y = -1;
d) 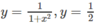
e) y = x 3 – 1 và tiếp tuyến với y = x 3 – 1 tại điểm (-1; -2).
Tính diện tích của hình phẳng giới hạn bởi các đường sau:
y
1
x
+
1
,x1 và tiếp tuyến với đường
y
1
x
+
1
tại điểm (2; 3/2)
Đọc tiếp
Tính diện tích của hình phẳng giới hạn bởi các đường sau: y = 1 x + 1 ,x=1 và tiếp tuyến với đường y = 1 x + 1 tại điểm (2; 3/2)
Diện tích hình phẳng P giới hạn bởi các đường: y 1 = x, y 2 = 2x, y 3 = 2 - x bằng:
A. 1 B. 2/3
C. 2 D. 1/3
Diện tích hình phẳng P giới hạn bởi các đường: y 1 = x, y 2 = 2x, y 3 = 2 - x bằng:
A. 1 B. 2/3
C. 2 D. 1/3
Tính các tích phân sau:
∫
0
π
4
x
sin
x
+
(
x
+
1
)
cos
x
xsinx
+
cosx...
Đọc tiếp
Tính các tích phân sau: ∫ 0 π 4 x sin x + ( x + 1 ) cos x xsinx + cosx d x
Xét vị trí tương đối các cặp đường thẳng d và d cho bởi các phương trình sau:
a
)
d
:
x
-
3
+
2
t
y
-
2
+...
Đọc tiếp
Xét vị trí tương đối các cặp đường thẳng d và d' cho bởi các phương trình sau: a ) d : x = - 3 + 2 t y = - 2 + 3 t z = 6 + 4 t d ' : x = 5 + t ' y = - 1 - 4 t ' z = 20 + t '
b ) d : x = 1 + t y = 2 + t z = 3 - t d ' : x = 1 + 2 t ' y = - 1 + 2 t z = 2 - 2 t '
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) 0, F(2) 1, G(2) 1 và
∫
0
2
F
(
x
)
g
(
x
)
d
x
3 . Tính tích phân hàm:
∫
0
2
G
(
x
)
f
(
x
)
d
x
A. I 3. B. I 0....
Đọc tiếp
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
trong các hàm số sau hàm số nào đồng biến trên R: A. y= 2x-1/x+2 B. y= -x^3+x^2-5x C. y= x^3+2x+1 D.-x^4-2x^2+3
Xét tính hội tụ phân kỳ của tích phân:
I = \(\int\limits^{+\text{∞}}_1\dfrac{x^2-1}{x^4+1}dx\)