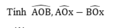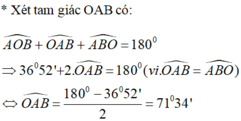Các câu hỏi tương tự
a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:y 2x (1); y 0,5x (2); y -x + 6 (3)b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.c) Tính các góc của tam giác OAB.Hướng dẫn câu c)Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.
T
í
n
h
AOB
^
,
AOx
^...
Đọc tiếp
a) Vẽ đồ thị các hàm số sau trên cùng một mặt phẳng tọa độ:
y = 2x (1); y = 0,5x (2); y = -x + 6 (3)
b) Gọi các giao điểm của đường thẳng có phương trình (3) với hai đường thẳng có phương trình (1) và (2) theo thứ tự là A và B. Tìm tọa độ của hai điểm A và B.
c) Tính các góc của tam giác OAB.
Hướng dẫn câu c)
Tính OA, OB rồi chứng tỏ tam giác OAB là tam giác cân.
T í n h AOB ^ , AOx ^ − BOx ^
Cho tam giác OAB cân tại A vẽ đường cao ah,bk biết canh OA=10cm, góc AOH= 20 độ .tính các cạnh của tam giác AKB giúp mik với
Cho góc xOy hai điểm A, B thứ tự chuyển động trên Ox, Oy đường tròn nội tiếp tam giác OAB tiếp xúc với OA, OB ở E,F
a, Chứng minh răng OE = OF = ( OA + OB - AB ) /2
b, Nếu chu vi tam giác OAB không đổi chứng minh AB luôn tiếp xúc với đường tròn cố định
tam giác OAB có góc O =120, OA=a, OB=b, OC là đường phân giác của góc O, OC =c, cmr 1/a+1/b=1/c
bài 1: cho hình thang vuông ABCD (vuông tại A và D ) có 2 đường chéo vuông góc với nhau tại O , AB=4cm , CD=9cm.
a) CMR : tam giác OAB đồng dạng với tam giác DAB
b) Tính độ dài AD
c) CM : tam giác OAB đồng dạng với tam giác OCD
d) Tính tỉ số diện tích của tam giác OAB và OCD
cho ba đường thẳng d1:y=3x,d2:y=1/3x,d3:y=-x+4 a,vẽ d1,d2,d3 trên cùng mặt phẳng toạ độ b,gọia,b lần lượt là giao điểm của d1 và d2.tìm toạ độ của a và b c,chứng minh tam giác OAB cân d,tính diện tích tam giác OAB
Cho tam giác OAB có góc O = 120 độ, OC là đường phân giác trong. CMR: \(\frac{1}{OA}+\frac{1}{OB}=\frac{1}{OC}\)
Cho đường tròn (O) và điểm A cách O một khoảng bằng 2R, kẻ tiếp tuyến AB tới đường tròn (B là tiếp điểm).
1) Tính số đo các góc của tam giác OAB.
2) Gọi C là điểm đối xứng với B qua OA. Chứng minh điểm C nằm trên đường tròn O và AC là tiếp tuyến của đường tròn (O).
3) Đoạn thẳng AO cắt đường tròn (O) tại G. Chứng minh G là trọng tâm tam giác ABC.
Bài 2: Cho đường tròn (O) bán kính OA=6cm. Dây BC của đường tròn vuông góc với OA tại trung điểm I của OA
a) C/m tam giác OAB đều
b) Tính độ dài BC