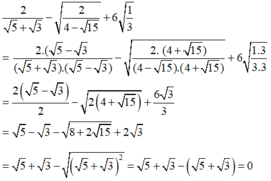Các câu hỏi tương tự
1, tính a/ (3+√5)(√10 - √2)√(3-√5)b/[√2-√(3-√5)].√2c/(√10 + √6).√(8-2√15)2, tìm x biết a/ √(x+5)1+√xb/√x + √(x-1)1c/ √(3-x) + √(x-5)103, phân tích đa thức thành nhân tử:a/ ab+b√a+√a+1 với a ≥0b/ x-2√xy + y với x,y ≥ 0c/√xy + 2√x - 3√y -6 với x,y ≥ 04, chứng minh rằng a/ (4+√15).(√10-√6).√(4-√15)2b/ √a + √b √(a+b) (a,b0)5, Cho √(8-a) + √(5+a) 5 tính √[(8-a).(5+a)]6, rút gọn √(7+2√10)-√15P/s : mn giúp e với nha
Đọc tiếp
1, tính a/ (3+√5)(√10 - √2)√(3-√5)
b/[√2-√(3-√5)].√2
c/(√10 + √6).√(8-2√15)
2, tìm x biết a/ √(x+5)=1+√x
b/√x + √(x-1)=1
c/ √(3-x) + √(x-5)=10
3, phân tích đa thức thành nhân tử:
a/ ab+b√a+√a+1 với a ≥0
b/ x-2√xy + y với x,y ≥ 0
c/√xy + 2√x - 3√y -6 với x,y ≥ 0
4, chứng minh rằng a/ (4+√15).(√10-√6).√(4-√15)=2
b/ √a + √b > √(a+b) (a,b>0)
5, Cho √(8-a) + √(5+a) = 5 tính √[(8-a).(5+a)]
6, rút gọn √(7+2√10)-√15
P/s : mn giúp e với nha
Đưa thừa số vào trong dấu căn:
c) 1/y√19yvới y >0 y d) 1 /3y√27/y2 y với y <0
Rút gọn biểu thức:
b) y/2+ 3/4 √1 -4y+ 4y2 với y< 1/2
. Thực hiện phép tính:
a)( 2/√3-1 +3/√3-2 +15/3-√3 )*1/√3+5
b,(√14-√7/1-√2 +√15-√5/1-√3)*1/√7 -√5
Bài 5:So sánh (không dùng bảng số hay máy tính bỏ túi)a. 2 và √2+ 1 b. 1 và √3–1 c. 2√31và 10 d. -3.√11và -12Bài 6 : So sánh:a/ 15 và √200b/ 27 và 9 √5c/ -24 và -6 √15
Đọc tiếp
Bài 5:So sánh (không dùng bảng số hay máy tính bỏ túi)
a. 2 và √2+ 1 b. 1 và √3–1 c. 2√31và 10 d. -3.√11và -12
Bài 6 : So sánh
:a/ 15 và √200
b/ 27 và 9 √5
c/ -24 và -6 √15
1. CHỨNG MINH ĐẲNG THỨCa. text{[}3+2sqrt{6}-sqrt{33}text{]}cdottext{[}sqrt{22}+sqrt{6}+4text{]}24b. text{[}frac{1}{5-2sqrt{6}}+frac{2}{5+2sqrt{6}}text{]}cdottext{[}15+2sqrt{6}text{]}c.text{[}frac{4}{3}cdotsqrt{3}+sqrt{2}+sqrt{3frac{1}{3}}text{]}cdottext{[}sqrt{1,2}+sqrt{2}-4sqrt{frac{1}{5}}text{]}4d. sqrt{text{[}1-sqrt{1989}text{]}^2}cdotsqrt{1990+2sqrt{1989}}1988e. frac{a-sqrt{ab}+b}{asqrt{a}+bsqrt{b}}-frac{1}{a-b}frac{sqrt{a}-sqrt{b}-1}{a-b}với a0;b0và ane b
Đọc tiếp
1. CHỨNG MINH ĐẲNG THỨC
a. \(\text{[}3+2\sqrt{6}-\sqrt{33}\text{]}\cdot\text{[}\sqrt{22}+\sqrt{6}+4\text{]}=24\)
b. \(\text{[}\frac{1}{5-2\sqrt{6}}+\frac{2}{5+2\sqrt{6}}\text{]}\cdot\text{[}15+2\sqrt{6}\text{]}\)
c.\(\text{[}\frac{4}{3}\cdot\sqrt{3}+\sqrt{2}+\sqrt{3\frac{1}{3}}\text{]}\cdot\text{[}\sqrt{1,2}+\sqrt{2}-4\sqrt{\frac{1}{5}}\text{]}=4\)
d. \(\sqrt{\text{[}1-\sqrt{1989}\text{]}^2}\cdot\sqrt{1990+2\sqrt{1989}}=1988\)
e. \(\frac{a-\sqrt{ab}+b}{a\sqrt{a}+b\sqrt{b}}-\frac{1}{a-b}=\frac{\sqrt{a}-\sqrt{b}-1}{a-b}\)với \(a>0;b>0\)và \(a\ne b\)
Bài 1: Tínha) 5sqrt{8}-4sqrt{27}-2sqrt{75}+sqrt{108} b) 1sqrt{left(3-sqrt{6}right)^2}+sqrt{left(1-sqrt{6}right)^2} c) dfrac{5sqrt{3}-3sqrt{5}}{sqrt{5}-sqrt{3}}+dfrac{1}{4+sqrt{15}} d) dfrac{2sqrt{3-sqrt{5}}left(3+sqrt{5}right)}{sqrt{10}-sqrt{2}}-dfrac{sqrt{15}+sqrt{5}}{sqrt{12}+2} Bài 2: Cho (d₁): y dfrac{1}{2}x-4 và (d₂): y -3x+3 . Vẽ (d₁) và (d₂) trên cùng một hệ trục tọa độ. Tìm tọa độ giao điểm A của 2 đường thẳng trên. Helpp!!
Đọc tiếp
Bài 1: Tính
a) \(5\sqrt{8}-4\sqrt{27}-2\sqrt{75}+\sqrt{108}\)
b) \(1\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(1-\sqrt{6}\right)^2}\)
c) \(\dfrac{5\sqrt{3}-3\sqrt{5}}{\sqrt{5}-\sqrt{3}}+\dfrac{1}{4+\sqrt{15}}\)
d) \(\dfrac{2\sqrt{3-\sqrt{5}}\left(3+\sqrt{5}\right)}{\sqrt{10}-\sqrt{2}}-\dfrac{\sqrt{15}+\sqrt{5}}{\sqrt{12}+2}\)
Bài 2: Cho (d₁): y = \(\dfrac{1}{2}x-4\) và (d₂): y = \(-3x+3\) . Vẽ (d₁) và (d₂) trên cùng một hệ trục tọa độ. Tìm tọa độ giao điểm A của 2 đường thẳng trên.
Helpp!!
Phương pháp 5. Biến đổi về dạng tổng các bình phương \(A^2+B^2+C^2=0\)
a \(x+y+12=4\sqrt{x}+6\sqrt{y-1}\)
b \(x+y+z+35=2\left(2\sqrt{x+1}+3\sqrt{y+2}+4\sqrt{z+3}\right)\)
c \(9x+17=6\sqrt{8x+1}+4\sqrt{x+3}\)
d \(\sqrt{x}+2\sqrt{x+3}=x+4\)
e\(\sqrt{3-x}+2\sqrt{3x-2}-3=x\)
1. phân tích đa thức thành nhân tử
a)x^2-13
b)x+5√x +6(x≥0)
c)x-4√x +3(x≥0)
d) 3x-6√x -6(x≥0)
2 Tìm GTNN của:
a) A= x-√x +3
b) B=x+3√x +5
c) C=x^4-8xy-x^2y+x^2y^2-xy^2+y^4+2000
Giải giúp mình nha ^^
1/ Tính:
a)\(\sqrt{48}-6\sqrt{\frac{1}{3}}+\frac{\sqrt{3}-3}{\sqrt{3}}\)
b)\(\frac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}-\frac{5-2\sqrt{5}}{2\sqrt{5}-4}\)
2/ Tìm x:
a) \(\sqrt{4\left(1-x\right)^2}-12=0\)
b)\(\sqrt{4x^2-12x+9}=5\)
1.Cho xby+cz,yax+cz,zax+by,x+y+z khác 0.Tính:Qfrac{1}{1+a}+frac{1}{1+b}+frac{1}{c}2.Cho a+b+c0.C/m:a^4+b^4+c^4frac{1}{2}left(a^2+b^2+c^2right)3.Cho x+y+z0.C/m:2left(x^5+y^5+z^5right)5xyzleft(x^2+y^2+z^2right)4.Cho a,b,c đôi một khác nhau và khác 0 thỏa mãn:a+frac{1}{b}b+frac{1}{c}c+frac{1}{a}C/m:abc1 hoặc abc-15.Cho x+y+xy3,yz+y+z8,xz+x+z15.Tính x+y+z6. Cho xy+x+y-1 ;x^2y+xy^2-12Tính Px^3+y^37.Cho a,b,c khác 0:frac{ay-bx}{c}frac{cx-az}{b}frac{bz-cy}{a}C/m:left(ax+by+czright)^2left(x^2+y...
Đọc tiếp
1.Cho x=by+cz,y=ax+cz,z=ax+by,x+y+z khác 0.Tính:
Q=\(\frac{1}{1+a}+\frac{1}{1+b}+\frac{1}{c}\)
2.Cho a+b+c=0.C/m:\(a^4+b^4+c^4=\frac{1}{2}\left(a^2+b^2+c^2\right)\)
3.Cho x+y+z=0.C/m:\(2\left(x^5+y^5+z^5\right)=5xyz\left(x^2+y^2+z^2\right)\)
4.Cho a,b,c đôi một khác nhau và khác 0 thỏa mãn:\(a+\frac{1}{b}=b+\frac{1}{c}=c+\frac{1}{a}\)
C/m:abc=1 hoặc abc=-1
5.Cho x+y+xy=3,yz+y+z=8,xz+x+z=15.Tính x+y+z
6. Cho xy+x+y=-1 ;\(x^2y+xy^2=-12\)
Tính P=\(x^3+y^3\)
7.Cho a,b,c khác 0:\(\frac{ay-bx}{c}=\frac{cx-az}{b}=\frac{bz-cy}{a}\)
C/m:\(\left(ax+by+cz\right)^2=\left(x^2+y^2+z^2\right)\left(a^2+b^2+c^2\right)\)
bài 1: giải pt
a. \(\sqrt{x-1}+\sqrt{2x-1}=5\)
b. \(x+\sqrt{2x-1}-2=0\)
bài 2: tính
A= \(\sqrt{7-4\sqrt{3}}-\sqrt{7+4\sqrt{3}}\)
B=\(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}\)
C=\(\left(\frac{1}{3-\sqrt{5}}-\frac{1}{3+\sqrt{5}}\right).\frac{\sqrt{5}-1}{5-\sqrt{5}}\)