Hình 19:
Xét ΔABC có
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{BAC}+60^0+50^0=180^0\)
=>\(\widehat{BAC}=70^0\)
Ta có: AM là phân giác của góc BAC
=>\(\widehat{BAM}=\dfrac{1}{2}\cdot\widehat{BAC}\)
=>\(x=\dfrac{1}{2}\cdot70^0=35^0\)
Xét ΔMAB có góc AMC là góc ngoài tại đỉnh M
nên \(\widehat{AMC}=\widehat{MAB}+\widehat{MBA}\)
=>\(y=60^0+35^0=95^0\)
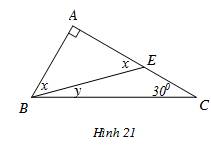
Hình 21:
Ta có: ΔABE vuông tại A
=>\(\widehat{ABE}+\widehat{AEB}=90^0\)
=>\(x+x=90^0\)
=>\(x=\dfrac{90^0}{2}=45^0\)
Xét ΔEBC có \(\widehat{AEB}\) là góc ngoài tại đỉnh E
nên \(\widehat{AEB}=\widehat{EBC}+\widehat{ECB}\)
=>\(y=45^0-30^0=15^0\)
Đúng 2
Bình luận (0)
