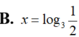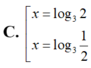Các câu hỏi tương tự
1.Tìm ba nghiệm x,y,z thoả mãn:(x-z).xy.(2x-3)100000.(x+2)100000-(y+z).(2x)y.(3x-5)99999,5.(5x-6)99999,5-(x-z).x2y.(4x-7)99999.(8x-12)99999-(y+z).xy.(2x-3)99998,5.(x+2)99998,5-...….......-(x-z).xy.(2x-3)2.(x+2)2-(y+z).(2x)y.(3x-5).(5x-6)-2.(x-z).x2y02.Tìm x thoả ma trận mắt xích đơn vị sau:p(x)|50000----p(x)|49999----...----p(x)|0----103.Số đơn vị cần thiết để chuyển hoá ánh xạ p(x) về vô cùng và về 04.Vùng khả tích cuả ptrình bậc cao ở câu 15.Công thức tìm trực chuẩn và độ biến thiên (Gợi ý:Áp...
Đọc tiếp
1.Tìm ba nghiệm x,y,z thoả mãn:
(x-z).xy.(2x-3)100000.(x+2)100000-(y+z).(2x)y.(3x-5)99999,5.(5x-6)99999,5-(x-z).x2y.(4x-7)99999.(8x-12)99999-(y+z).xy.(2x-3)99998,5.(x+2)99998,5-...….......-(x-z).xy.(2x-3)2.(x+2)2-(y+z).(2x)y.(3x-5).(5x-6)-2.(x-z).x2y=0
2.Tìm x thoả ma trận mắt xích đơn vị sau:
p(x)|50000----p(x)|49999----...----p(x)|0----1=0
3.Số đơn vị cần thiết để chuyển hoá ánh xạ p(x) về vô cùng và về 0
4.Vùng khả tích cuả ptrình bậc cao ở câu 1
5.Công thức tìm trực chuẩn và độ biến thiên
(Gợi ý:Áp dụng cthức cuả Povoni)
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2
1
và
d...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x+2y+3z-5=0. Đường thẳng Δ vuông góc với (P) cắt d1 và d2 có phương trình là:
![]()
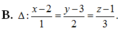
![]()
![]()
Cho hệ phương trình
x
+
y
m
-
1
x
2
+
y
2
-
2
x...
Đọc tiếp
Cho hệ phương trình x + y = m - 1 x 2 + y 2 - 2 x - 2 y = - 1 . Tìm m để hệ phương trình có nghiệm x 0 ; y 0 thỏa mãn P = x 0 2 + y 0 2 nhỏ nhất
![]()
![]()
![]()
![]()
Cho phương trình
m
.
l
n
2
(
x
+
1
)
-
(
x
+
2
-
m
)
l
n
(
x
+
1
)
-
x
-
2
0
(1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn
0...
Đọc tiếp
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Tìm các số thực x, y thỏa mãn:
a) 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
b) 4x + 3 + (3y – 2)i = y +1 + (x – 3)i
c) x + 2y + (2x – y)i = 2x + y + (x + 2y)i
Cho hàm số y f(x) có đạo hàm liên tục trên R, thỏa mãn
2
f
(
2
x
)
+
f
(
1
-
2
x
)
12
x
3
. Tìm phương trình tiếp tuyến của đồ thị hàm số y f(x) tại điểm có hoành độ x 1 A. B. C. D.
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm liên tục trên R, thỏa mãn 2 f ( 2 x ) + f ( 1 - 2 x ) = 12 x 3 . Tìm phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = 1
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Tìm tất cả các hàm số f: R -> R thoả mãn điều kiện:
f((x - y)2) = x2 - 2y.f(x) + (f(y))2, với mọi x, y thuộc R.
Trong không gian với hệ trục Oxyz, cho 2 đường thẳng lần lượt có phương trình:
d
1
:
y
x
-
2
2
y
-
2
1
z
-
3
3
;
d...
Đọc tiếp
Trong không gian với hệ trục Oxyz, cho 2 đường thẳng lần lượt có phương trình:
d 1 : y = x - 2 2 = y - 2 1 = z - 3 3 ; d 2 : y = x - 1 2 = y - 2 - 1 = z - 1 4
Mặt phẳng cách đều 2 đường thẳng d 1 , d 2 có phương trình là:
![]()
![]()
![]()
![]()
Biết
F
(
x
)
là một nguyên hàm của hàm số
f
(
x
)
x
8
-
x
2
thoả mãn
F
(
2
)
0
. Khi đó phương trình
F
(
x
)...
Đọc tiếp
Biết F ( x ) là một nguyên hàm của hàm số f ( x ) = x 8 - x 2 thoả mãn F ( 2 ) = 0 . Khi đó phương trình F ( x ) = x có nghiệm là
A. x = 3
B. x = 1
C. x = -1
D. Tất cả sai