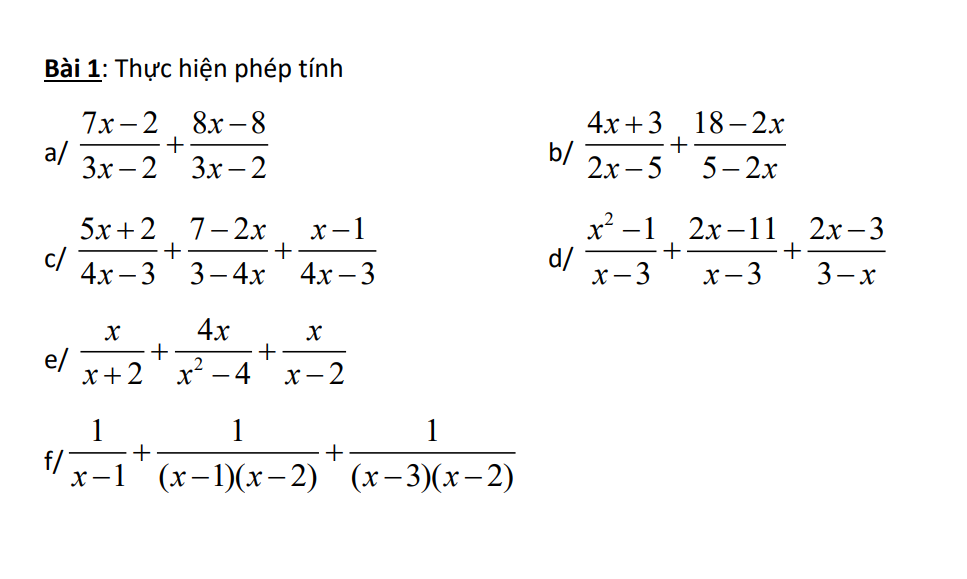\(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)=360\)
=>\(\left(x^2+5x+4\right)\left(x^2+5x+6\right)=360\)
=>\(\left(x^2+5x\right)^2+10\left(x^2+5x\right)+24-360=0\)
=>\(\left(x^2+5x\right)^2+10\left(x^2+5x\right)-336=0\)
=>\(\left(x^2+5x+24\right)\left(x^2+5x-14\right)=0\)
mà \(x^2+5x+24=\left(x+\dfrac{5}{2}\right)^2+\dfrac{71}{4}>=\dfrac{71}{4}>0\forall x\)
nên \(x^2+5x-14=0\)
=>(x+7)(x-2)=0
=>\(\left[{}\begin{matrix}x=-7\\x=2\end{matrix}\right.\)

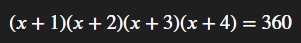 tìm x biết :
tìm x biết :