Đáp án D
Phương pháp giải:
Dựa vào điều kiện để hàm số b1 trên b1 đồng biến hoặc nghịch biến trên khoảng
Lời giải: Ta có 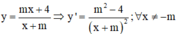
Yêu cầu bài toán 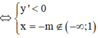
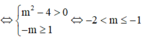
Đáp án D
Phương pháp giải:
Dựa vào điều kiện để hàm số b1 trên b1 đồng biến hoặc nghịch biến trên khoảng
Lời giải: Ta có 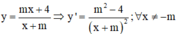
Yêu cầu bài toán 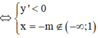
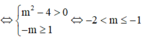
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x − 1 x − m nghịch biến trên khoảng − ∞ ; 2 .
A. 1 , + ∞
B. 2 , + ∞
C. 2 , + ∞
D. 1 , + ∞
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m 3 x 3 + 7 m x 2 + 14 x - m + 2 nghịch biến trên nửa khoảng [ 1 ; + ∞ ) ?
A. - ∞ ; - 14 15
B. ( - ∞ ; - 14 15 ]
C. - 2 ; - 14 15
D. [ - 14 15 ; + ∞ )
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x 3 3 + 7 m x 2 + 14 x - m + 2 nghịch biến trên [ 1 ; + ∞ )
A. - ∞ ; - 14 15
B. ( - ∞ ; - 14 15 ]
C. - 2 ; - 14 15
D. [ - 14 15 ; + ∞ )
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 - m x + 1 nghịch biến trên các khoảng mà nó xác định?
A. m ≤ 1 .
B.m<1
C.m<-3
D. m ≤ - 3 .
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 4 x + m nghịch biến trên khoảng ( - ∞ ; 1 ) ?
A. - 2 < m ≤ - 1
B. - 2 ≤ m ≤ - 1
C. - 2 ≤ m ≤ 2
D. - 2 < m < 2
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = m x + 4 x + m nghịch biến trên khoảng − ∞ ; 1 ?
A. − 2 ≤ m ≤ 2
B. -2 < m < 2
C. − 2 < m ≤ − 1
D. − 2 ≤ m ≤ − 1
Tìm tất cả các giá trị thực của tham số m để hàm số y = - x 3 + 2 x 2 - m - 1 x + 2 nghịch biến trên khoảng - ∞ ; + ∞
A. m ≤ 7 3
B. m ≥ 7 3
C. m ≥ 1 3
D. m > 7 3
Tìm tất cả các giá trị thực của tham số m để hàm số y = 2 + m x 2 x + m nghịch biến trên từng khoảng xác định của nó
A. m ≤ - 2 m ≥ 2
B. - 2 < m < 2
C. - 2 ≤ m ≤ 2
D. m < - 2 m > 2
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = - 1 3 x 3 - m x 2 + 2 m - 3 x - m + 2 luôn nghịch biến trên R.
A. m ∈ - ∞ ; - 3 ∪ 1 ; + ∞
B. - 3 ≤ m ≤ 1
C. m ≤ 1
D. - 3 < m < 1