Các câu hỏi tương tự
Cho hàm số
y
x
-
2
x
2
+
m
x
+
m
2
-
3
Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt là A. -2 m -1 B. ...
Đọc tiếp
Cho hàm số y = x - 2 x 2 + m x + m 2 - 3 Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ba điểm phân biệt là
A. -2 < m < -1
B. - 2 < m < 2 m ≠ - 1
C. -1 < m < 2
D. - 1 < m < 2 m ≠ - 1
Cho hàm số
y
m
x
3
-
x
2
-
2
x
+
8
m
có đồ thị (C) . Tìm tất cả giá trị tham số m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt. A.
m
∈
-
1
6
;
1
2
B.
m
∈...
Đọc tiếp
Cho hàm số y = m x 3 - x 2 - 2 x + 8 m có đồ thị (C) . Tìm tất cả giá trị tham số m để đồ thị (C) cắt trục hoành tại ba điểm phân biệt.
A. m ∈ - 1 6 ; 1 2
B. m ∈ - 1 6 ; 1 2
C. m ∈ - 1 6 ; 1 2 / 0
D. m ∈ - ∞ ; 1 2 / 0
Cho hàm số
y
1
3
x
3
-
m
x
2
-
x
+
m
+
2
3
có đồ thị (C) . Tất cả các giá trị của tham số m để (C) cắt trục Ox tại ba điểm phân biệt có hoành độ x1; x2; x3 thỏa
x
1
2
+
x...
Đọc tiếp
Cho hàm số y = 1 3 x 3 - m x 2 - x + m + 2 3 có đồ thị (C) . Tất cả các giá trị của tham số m để (C) cắt trục Ox tại ba điểm phân biệt có hoành độ x1; x2; x3 thỏa x 1 2 + x 2 2 + x 3 2 > 15 là
A. m>1 hoặc m<-1
B. m< -1
C. m>0
D. m>1
Cho hàm số
y
x
3
-
m
x
+
1
(với m là tham số). Tìm tất cả các giá trị của m để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt. A.
m
≤
3
2
3
2
B.
m
3
2...
Đọc tiếp
Cho hàm số y = x 3 - m x + 1 (với m là tham số). Tìm tất cả các giá trị của m để đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
A. m ≤ 3 2 3 2
B. m > 3 2 3 2
C. m < 3 2 3 2
D. m ≥ 3 2 3 2
Cho hàm số
y
-
x
4
+
2
x
2
+
m
. Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt là A. 0 m 1 B.
-
1
m
≤
0
C. -1 m 0 D.
-
1
≤
m
0
Đọc tiếp
Cho hàm số y = - x 4 + 2 x 2 + m . Tất cả giá trị của tham số m để đồ thị hàm số đã cho cắt trục hoành tại ít nhất ba điểm phân biệt là
A. 0 < m < 1
B. - 1 < m ≤ 0
C. -1 < m < 0
D. - 1 ≤ m < 0
Cho hàm số
f
(
x
)
x
3
-
3
x
2
. Tính tổng tất cả các giá trị nguyên của m để đồ thị hàm số
g
(
x
)
f
(
x
)
+
m
cắt trục hoành tại 4 điểm phân biệt. A. 3 B. 10 C. 4 D. 6
Đọc tiếp
Cho hàm số f ( x ) = x 3 - 3 x 2 . Tính tổng tất cả các giá trị nguyên của m để đồ thị hàm số g ( x ) = f ( x ) + m cắt trục hoành tại 4 điểm phân biệt.
A. 3
B. 10
C. 4
D. 6
Cho hàm số
y
f
(
x
)
liên tục trên R và có đồ thị như hình bên dưới Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình
f
x
4
m
+
2
log
4
2
có hai nghiệm dương phân...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có đồ thị như hình bên dưới
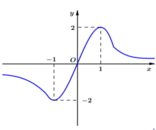
Biết rằng trục hoành là tiệm cận ngang của đồ thị. Tìm tất cả các giá trị thực của tham số m để phương trình f x = 4 m + 2 log 4 2 có hai nghiệm dương phân biệt
![]()
![]()
![]()
![]()
Cho (C) là đồ thị của hàm số y(x-2)/(x+1) và đường thẳng d:ymx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C) A. B. C. D.
Đọc tiếp
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y
x
3
+
(
m
+
2
)
x
2
+
(
m
2
m
-
3
)
x
-
m
2
cắt trục hoành tại ba điểm phân biệt? A. 3 B.. 4 C. 1 D. 2
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt?
A. 3
B.. 4
C. 1
D. 2



