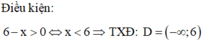Các câu hỏi tương tự
Tìm tập xác định D của hàm số
y
log
x
2
+
5
x
-
6
A.
D
-
6
;
1
B.
D
-
∞
;...
Đọc tiếp
Tìm tập xác định D của hàm số y = log x 2 + 5 x - 6
A. D = - 6 ; 1
B. D = - ∞ ; - 6 ∪ [ 1 ; + ∞ )
C. D = [-6;1]
D. D = - ∞ ; - 6 ∪ 1 ; + ∞
Tìm tập xác định D của hàm số
y
(
x
2
-
13
x
+
22
)
-
6
A.
D
{
2
;
11
}
B.
D
ℝ
{
2
;...
Đọc tiếp
Tìm tập xác định D của hàm số y = ( x 2 - 13 x + 22 ) - 6
A. D = { 2 ; 11 }
B. D = ℝ \ { 2 ; 11 }
C. D = ℝ \ ( 2 ; 11 )
D. D = { 2 ; 11 }
Tìm tập xác định
D
ℝ
của hàm số
y
log
2
x
+
1
-
1
A.
D
(
-
∞
;
1
]
B.
D
3
;
+
∞...
Đọc tiếp
Tìm tập xác định D = ℝ của hàm số y = log 2 x + 1 - 1
A. D = ( - ∞ ; 1 ]
B. D = 3 ; + ∞
C. D = [ 1 ; + ∞ )
D. D = ℝ \ 3
Cho hàm số
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
,
(
a
,
b
,
c
,
d
∈
ℝ
)
thỏa mãn
a
0
,
d
0
2018
,
a
+...
Đọc tiếp
Cho hàm số f ( x ) = a x 3 + b x 2 + c x + d , ( a , b , c , d ∈ ℝ ) thỏa mãn a > 0 , d > 0 > 2018 , a + b + c + d - 2018 < 0 Tìm số điểm cực trị của hàm số y = f ( x ) - 2018
A. 2
B. 1
C. 3
D. 5
Hàm số
y
ln
x
2
−
2
m
x
+
4
có tập xác định
D
ℝ
khi các giá trị của tham số m là A.
m
2
B.
m
−...
Đọc tiếp
Hàm số y = ln x 2 − 2 m x + 4 có tập xác định D = ℝ khi các giá trị của tham số m là
A. m < 2
B. m < − 2 m > 2
C. m = 2
D. − 2 < m < 2
Cho hàm số yf(x) xác định và liên tục trên tập
D
ℝ
{
-
1
}
và có bảng biến thiên:Dựa vào bảng biến thiên của hàm số yf(x) Khẳng định nào sau đây là khẳngđịnh sai? A. Giá trị nhỏ nhất của hàm số trên đoạn
[
1
;
8
]
bằng -2 B. Phương trình f(x)m có 3 nghiệm thực phân biệt khi x -2 C. Hàm số đạt cực tiểu tại x3 D. Hàm số nghịch biến trên khoảng
(
-...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên tập D = ℝ \ { - 1 } và có bảng biến thiên:
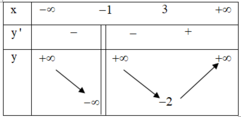
Dựa vào bảng biến thiên của hàm số y=f(x) Khẳng định nào sau đây là khẳng
định sai?
A. Giá trị nhỏ nhất của hàm số trên đoạn [ 1 ; 8 ] bằng -2
B. Phương trình f(x)=m có 3 nghiệm thực phân biệt khi x > -2
C. Hàm số đạt cực tiểu tại x=3
D. Hàm số nghịch biến trên khoảng ( - ∞ ; 3 )
Tập
D
ℝ
k
π
2
k
∈
ℤ
là tập xác định của hàm số nào sau đây? A.
y
cot
x
B.
y
cot
2
x
C.
y
tan
x
D....
Đọc tiếp
Tập D = ℝ \ k π 2 k ∈ ℤ là tập xác định của hàm số nào sau đây?
A. y = cot x
B. y = cot 2 x
C. y = tan x
D. y = tan 2 x
Cho hàm số
y
f
(
x
)
xác định và liên tục trên tập
D
ℝ
1
và có bảng biến thiênDựa vào bảng biến thiên của hàm số
y
f
x
. Khẳng định nào sau đây là sai? A. Phương trình
f
x
m
có 3 nghiệm thực phân biệt khi x -2 B. Giá trị nhỏ nhất của hàm s...
Đọc tiếp
Cho hàm số y = f ( x ) xác định và liên tục trên tập D = ℝ \ 1 và có bảng biến thiên
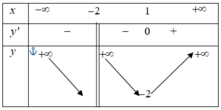
Dựa vào bảng biến thiên của hàm số y = f x . Khẳng định nào sau đây là sai?
A. Phương trình f x = m có 3 nghiệm thực phân biệt khi x > -2
B. Giá trị nhỏ nhất của hàm số trên đoạn 0 ; 6 là -2
C. Hàm số đạt cực tiểu tại x = 1
D. Hàm số nghịch biến trên khoảng − ∞ ; 1
Tập xác định của hàm số
y
log
2
2
x
1
-
x
2
có dạng
[
a
;...
Đọc tiếp
Tập xác định của hàm số y = log 2 2 x 1 - x 2 có dạng [ a ; b ) ∪ [ c ; d ) Tính a + b + c + d.
A. 1.
B. -2.
C. 3.
D. -4.
Tìm tập xác định D của hàm số
y
x
2
−
x
−
2
−
3
A.
D
−
∞
;
−
1
∪
2...
Đọc tiếp
Tìm tập xác định D của hàm số y = x 2 − x − 2 − 3
A. D = − ∞ ; − 1 ∪ 2 ; + ∞
B. D = ℝ \ − 1 ; 2
C. D = ℝ
D. D = 0 ; + ∞