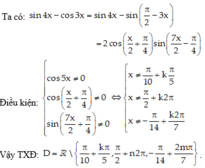Các câu hỏi tương tự
Tính đạo hàm của hàm số: y = tan π / 2 – x với x ≠ k π , k ∈ Z
Dựa vào các công thức cộng đã học:
sin(a + b) = sina cosb + sinb cosa;
sin(a – b) = sina cosb - sinb cosa;
cos(a + b) = cosa cosb – sina sinb;
cos(a – b) = cosa cosb + sina sinb;
và kết quả cos π/4 = sinπ/4 = √2/2, hãy chứng minh rằng:
a) sinx + cosx = √2 cos(x - π/4);
b) sin x – cosx = √2 sin(x - π/4).
Cho hàm số
y
cos
2
x
.a) Chứng minh rằng cos
2
x
+
k
π
cos
2
x
với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số
y
cos
2
x
.b) Viết phương...
Đọc tiếp
Cho hàm số y = cos 2 x .
a) Chứng minh rằng cos 2 x + k π = cos 2 x với mọi số nguyên k. Từ đó vẽ đồ thị (C) của hàm số y = cos 2 x .
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = π / 3 .
c) Tìm tập xác định của hàm số : z = 1 - cos 2 x 1 + cos 2 2 x
trang 40 SGK Toán 11 tập 1 - Kết nối tri thức
15 tháng 7 2023 lúc 12:46
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
Giải các pt: A, cos(4x + π/3)=✓3/2. ;. B, sin^2x-3sin3x+2=0. ;. C, tan(2x+10°)=√3. ;. D, tanx.cot2x=1
Số nghiệm của phương trình
sin
x
.
sin
2
x
+
2
.
sin
x
.
cos
2...
Đọc tiếp
Số nghiệm của phương trình sin x . sin 2 x + 2 . sin x . cos 2 x + sin x + cos x sin x + cos x = 3 . cos 2 x trong khoảng - π , π là:
A. 2
B. 4
C. 3
D. 5
Rút gọn biểu thức D= sin(5π+x)+cos(x-π/2)+cot(3π-x)+tan(3π/2-x)
Tập xác định của hàm số y=cotx/cosx-1 A . R\{kpi/2 , k thuộc z} B . R\{pi/2+kpi,k thuộc z} C . R\{kpi,k thuộc z} D . R
Cho hàm số y sin4xa) Chứng minh rằng sin4(x + kπ/2) sin4x với k ∈ ZTừ đó vẽ đồ thị của hàm sốy sin4x; (C1)y sin4x + 1. (C2)b) Xác định giá trị của m để phương trình: sin4x + 1 m (1)- Có nghiệm- Vô nghiệmc) Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ
x
0
π
/
24
Đọc tiếp
Cho hàm số y = sin4x
a) Chứng minh rằng sin4(x + kπ/2) = sin4x với k ∈ Z
Từ đó vẽ đồ thị của hàm số
y = sin4x; (C1)
y = sin4x + 1. (C2)
b) Xác định giá trị của m để phương trình: sin4x + 1 = m (1)
- Có nghiệm
- Vô nghiệm
c) Viết phương trình tiếp tuyến của (C2) tại điểm có hoành độ x 0 = π / 24
1. tập xác định của hàm số ysqrt{sin8x+5}A. DRB. DRleft{-k2pi,kvarepsilon Zright}C. DRleft{-dfrac{pi}{2}+k2pi,kvarepsilon Zright}D. DRleft{-pi+k2pi,kvarepsilon Zright}2. giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số ysqrt{sin3x}A. M1;m-3B. M3;m1C. M1;m-1D. M1;m0left{-k2pi,kvarepsilon Zright}left{-k2pi,kvarepsilon Zright}
Đọc tiếp
1. tập xác định của hàm số \(y=\sqrt{sin8x+5}\)
A. D=R
B. D=R\\(\left\{-k2\pi,k\varepsilon Z\right\}\)
C. D=R\\(\left\{-\dfrac{\pi}{2}+k2\pi,k\varepsilon Z\right\}\)
D. D=R\\(\left\{-\pi+k2\pi,k\varepsilon Z\right\}\)
2. giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số \(y=\sqrt{sin3x}\)
A. M=1;m=-3
B. M=3;m=1
C. M=1;m=-1
D. M=1;m=0
\(\left\{-k2\pi,k\varepsilon Z\right\}\)\(\left\{-k2\pi,k\varepsilon Z\right\}\)