Các câu hỏi tương tự
Cho phương trình
(
m
-
5
)
.
3
x
+
(
2
m
-
2
)
.
2
x
.
3
x
+
(
1
-
m
)
.
4
x
0
, tập hợp tất cả các giá trị của tham số m để phương trì...
Đọc tiếp
Cho phương trình ( m - 5 ) . 3 x + ( 2 m - 2 ) . 2 x . 3 x + ( 1 - m ) . 4 x = 0 , tập hợp tất cả các giá trị của tham số m để phương trình có hai nghiệm phân biệt là khoảng (a;b). Tính S=a+b
A.4
B.5
C.6
D.8
Tìm tập hợp nghiệm của phương trình: 5. 4 x - 7. 10 x + 2. 25 x = 0
A. {1; 1/5} B. {1; 5/2}
C. {0;1} D. {0;-1}
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Cho phương trình (m + 1) 16x - 2( 2m - 3) .4x + 6m + 5 0 với m là tham số thực. Tập tất cả các giá trị của m để phương trình có hai nghiệm trái dấu có dạng (a; b). Tính P a.b A. 4 B. -4 C. 5 D. -5
Đọc tiếp
Cho phương trình (m + 1) 16x - 2( 2m - 3) .4x + 6m + 5 = 0 với m là tham số thực. Tập tất cả các giá trị của m để phương trình có hai nghiệm trái dấu có dạng (a; b). Tính P = a.b
A. 4
B. -4
C. 5
D. -5
Cho phương trình
m
x
2
-
2
x
+
2
+
1
-
x
2
+
2...
Đọc tiếp
Cho phương trình m x 2 - 2 x + 2 + 1 - x 2 + 2 x = 0 (m là tham số). Biết rằng tập hợp tất cả các giá trị của tham số m để phương trình trên có nghiệm thuộc đoạn 0 ; 1 + 2 2 là đoạn a ; b . Tính giá trị biểu thức T = 2 b - a
A. T = 4
B. T = 7 2
C. T = 3
D. T = 1 2
Giá trị nhỏ nhất của hàm số f(x) = x +1/x trên nửa khoảng [2;+••] A:2 B:5/2 C:0 D:7/2
Tìm tất cả các giá trị của tham số a để phương trình sau có nghiệm duy nhất
a
log
3
x
3
+
4
log
3
x
8
+
a
+
1
0
A. a1. B. a-1. C. Không tồn tại a. D. a1.
Đọc tiếp
Tìm tất cả các giá trị của tham số a để phương trình sau có nghiệm duy nhất a log 3 x 3 + 4 log 3 x 8 + a + 1 = 0
A. a=1.
B. a<-1.
C. Không tồn tại a.
D. a<1.
Cho hàm số \(f\left(x\right)=\frac{1}{5}m^2x^5-\frac{1}{3}mx^3+10x^2-\left(m^2-m-20\right)x\)Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên R. Tổng giá trị của tất cả các phần tử thuộc S bằng :
A. 3/2
B. -2
C. 5/2
D. 1/2
Cho hàm số
y
f
(
x
)
a
x
4
+
b
x
2
+
c
(
a
≠
0
)
có đồ thị như hình bên. Tất cả các giá trị của m để phương trình
f
(
x
)
+
m
+
1
0...
Đọc tiếp
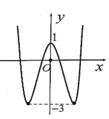
Cho hàm số y = f ( x ) = a x 4 + b x 2 + c ( a ≠ 0 ) có đồ thị như hình bên. Tất cả các giá trị của m để phương trình f ( x ) + m + 1 = 0 có 7 nghiệm phân biệt là:
A. m=-2.
B. m=-1.
C. m=2.
D. m=0.
Gọi S (a; b) là tập tất cả các giá trị của tham số thực m để phương trình
log
2
(
m
x
-
6
x
3
)
+
log
1
2
(
-
14
x
2
+
29
x
-
2
)
0
có 3 nghiệm phân biệt. Khi đó hiệu H b-a...
Đọc tiếp
Gọi S = (a; b) là tập tất cả các giá trị của tham số thực m để phương trình
log 2 ( m x - 6 x 3 ) + log 1 2 ( - 14 x 2 + 29 x - 2 ) = 0 có 3 nghiệm phân biệt. Khi đó hiệu H = b-a bằng
A. 5 2
B. 1 2
C. 2 3
D. 5 3