Gọi điểm cách đều hai đường thẳng (Δ1) và (Δ2) là M(x, y).
Ta có:
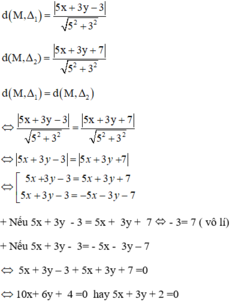
Vậy tập hợp các điểm M cách đều hai đường thẳng đã cho là đường thẳng: 5x + 3y + 2 = 0.
Gọi điểm cách đều hai đường thẳng (Δ1) và (Δ2) là M(x, y).
Ta có:
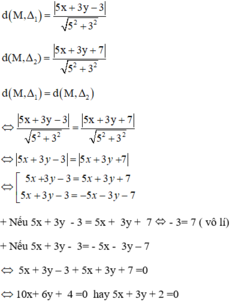
Vậy tập hợp các điểm M cách đều hai đường thẳng đã cho là đường thẳng: 5x + 3y + 2 = 0.
Tính góc giữa hai đường thẳng ∆1 và ∆2 trong trường hợp sau: Δ1: 2x + y – 4 = 0 và Δ2 : 5x – 2y + 3 = 0.
Góc giữa hai đường thẳng Δ1: 5x - y + 2 = 0 và Δ2: 3x + 2y + 1 = 0 là:
A. 30 °
B. 90 °
C. 45 °
D. 0 °
Quỹ tích các điểm cách đều hai đường thẳng d1: 5x-12y+4=0, d2: 4x-3y+2=0 là:
A. 9x + 7y + 2 = 0 và 7x – 9y = 0
B. 9x – 7y + 2 = 0 và 77x – 99y + 46 = 0
C. 9x – 7y + 2 = 0 và 7x + 9y = 0
D. 9x + 7y + 2 = 0 và 77x – 99y + 46 = 0
Cho ba đường thẳng d 1 : 3 x − 4 y + 1 = 0 , d 2 : 5 x + 3 y − 1 = 0 , d 3 : x + y + 6 = 0 . Số điểm M cách đều ba đường thẳng trên là
A.1
B. 2
C.3
D. 4
Cosin của góc giữa hai đường thẳng Δ1: a1x + b1y + c1 = 0 và Δ2: a2x + b2y + c2 = 0 là:
A. cos ( ∆ 1 ; ∆ 2 ) = a 1 b 1 + a 2 b 2 a 1 2 + b 1 2 . a 2 2 + b 2 2
B. cos ( ∆ 1 ; ∆ 2 ) = a 1 a 2 + b 1 b 2 a 1 2 + a 2 2 . b 1 2 + b 2 2
C. cos ( ∆ 1 ; ∆ 2 ) = a 1 a 2 + b 1 b 2 a 1 2 + b 1 2 . a 2 2 + b 2 2
D. cos ( ∆ 1 ; ∆ 2 ) = a 1 a 2 + b 1 b 2 a 1 2 + b 1 2 . a 2 2 + b 2 2
Côsin góc giữa 2 đường thẳng Δ1: x + 2y - 2 = 0 và Δ2: x - y = 0 là:
A. 10 10
B. 2
C. 2 3
D. 3 3
Tính góc giữa hai đường thẳng ∆1 và ∆2 trong các trường hợp sau: Δ1: y = –2x + 4 và Δ2: y = x 2 + 3 2
1. Cho M(3;-1) và đường thẳng d: 3x-4y+12=0. Tìm N đối xứng với M qua d.
2. Cho M(8;2) và đường thẳng d: 2x-3y+3=0. Tìm N đối xứng với M qua d.
3. Cho đường thẳng d: x+y-5=0 và I(2;0). Tìm điểm M thuộc d sao cho MI=3.
4. Cho tam giác ABC có M(2;-1) là trung điểm AB. Đường trung tuyến và đường cao qua A lần lượt là: d1: x+y-7=0 và d2: 5x+3y-29=0.
a.Tìm điểm A và viết pt cạnh BC.
b. Viết pt cạnh AC.
CÁC BẠN GIẢI GIÚP MÌNH VỚI NHÉ. CẢM ƠN
Cho 3 đường thẳng (d1) x=1-2t y=1+t, (d2): 3x+4y-4=0, (d3): 4x-3y+2=0 . Tìm điểm M nằm trên (d1) cách đều (d2) và d3