Chọn A.
Gọi z = a + bi khi đó ![]()
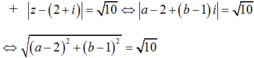
Hay (a – 2)2 + (b – 1)2 = 10
![]()
Từ (*) và (**) 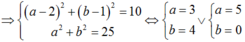
Vậy z = 3 + 4i hoặc z = 5.
Chọn A.
Gọi z = a + bi khi đó ![]()
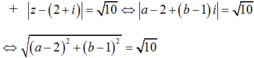
Hay (a – 2)2 + (b – 1)2 = 10
![]()
Từ (*) và (**) 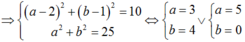
Vậy z = 3 + 4i hoặc z = 5.
Cho số phức z thỏa mãn | z -3 - 4i| = 5 .Tìm |z| để biểu thức: P = |z + 2|2 - |z – i|2 đạt giá trị lớn nhất?
![]()
B. 10
![]()
![]()
Biết các số phức z thỏa mãn |z-3|=|z+4i|. Tìm w m i n biết w = z + 4i -3
A. w m i n = 7 5
B. w m i n = 7 10
C. w m i n = 7 12
D. w m i n = 7
Biết số phức z thỏa mãn đồng thời hai điều kiện z - 3 - 4 i = 5 và biểu thức M = | z + 2 | 2 - | z - i | 2 đạt giá tri lớn nhất. Tính môđun của số phức z+i
![]()
![]()
![]()
![]()
Biết số phức z thỏa mãn z - 3 - 4 i = 5 và biểu thức T = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Tính z
A. z = 33
B. z = 50
C. z = 10
D. z = 5 2
Biết số phức z thỏa mãn đồng thời hai điều kiện: z - 3 - 4 i = 5 và biểu thức M = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Tính môđun của số phức z +i.
A. z + i = 61
B. z + i = 5 2
C. z + i = 3 5
D. z + i = 2 41
Biết số phức z thỏa mãn điều kiện z - 3 - 4 i = 5 và biểu thức P = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Tính z
![]()
![]()
![]()
![]()
Tìm số phức z sao cho z - 3 + 4 i = 5 và biểu thức P = z + 2 2 - z - i 2 đạt giá trị lớn nhất.
A. z = 5 +5i
B. z = 2 +i
C. z = 2 +2i
D. z = 4 +3i
Tìm số phức z thỏa mãn hai điều kiện:| z + 1 - 2i| = | z ¯ + 3 + 4i| và z - 2 i z ¯ + i là một số thuần ảo.
![]()
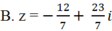
![]()
![]()
Cho số phức z thỏa mãn |z - 3 - 4i| = 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = | z + 2 | 2 - | z - i | 2 . Tính môđun của số phức w = M + mi ?
A. |w| = 2315
B. |w| = 1258
C. |w| = 3 137
D. |w| = 2 309
Cho số phức z thoả mãn z - 3 - 4 i = 5 và biểu thức P = z + 2 2 - z - i 2 đạt giá trị lớn nhất. Môđun của số phức z bằng
A.10.
B. 5 2
C.13.
D. 10 .