Các câu hỏi tương tự
Cho số thực dương k 0 thỏa mãn
∫
0
2
d
x
x
2
+
k
ln
(
2
+
5
)
. Mệnh đề nào sau đây đúng?
Đọc tiếp
Cho số thực dương k > 0 thỏa mãn ∫ 0 2 d x x 2 + k = ln ( 2 + 5 ) . Mệnh đề nào sau đây đúng?
![]()
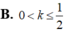
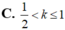
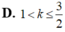
n là số nguyên dương và k là tích của tất cả các số nguyên từ 1 đến n. Nếu k là bội số của 1440 thì giá trị nhỏ nhất có thể có của n là A. 8 B. 12 C. 16 D. 18 E. 24
Giá trị k thỏa mãn đường thẳng
d
:
y
k
x
+
k
cắt đồ thị
H
:
y
x
-
4
2
x
-
2
tại hai điểm phân biệt A, B cùng cách đều đường thẳng y 0. Khi đó, k thuộc khoảng nào trong các khoảng sau đây?
Đọc tiếp
Giá trị k thỏa mãn đường thẳng d : y = k x + k cắt đồ thị H : y = x - 4 2 x - 2 tại hai điểm phân biệt A, B cùng cách đều đường thẳng y = 0. Khi đó, k thuộc khoảng nào trong các khoảng sau đây?
![]()
![]()
![]()
![]()
Gọi d là đường thẳng đi qua điểm A( -1; 0) với hệ số góc k . Tìm k để đường thẳng d cắt đồ thị hàm số C: y x3-3x2+ 4 tại ba điểm phân biệt A; B; C và tam giác OBC có diện tích bằng 1? A. k 2 B. k -1 C. k 1 D. Đáp án khác
Đọc tiếp
Gọi d là đường thẳng đi qua điểm A( -1; 0) với hệ số góc k . Tìm k để đường thẳng d cắt đồ thị hàm số C: y= x3-3x2+ 4 tại ba điểm phân biệt A; B; C và tam giác OBC có diện tích bằng 1?
A. k =2
B. k= -1
C. k= 1
D. Đáp án khác
Với k và n là hai số nguyên dương tùy ý thỏa mãn k
≤
n. Mệnh đề nào dưới đây đúng? A. . B. . C. D..
Đọc tiếp
Với k và n là hai số nguyên dương tùy ý thỏa mãn k ≤ n. Mệnh đề nào dưới đây đúng?
A. 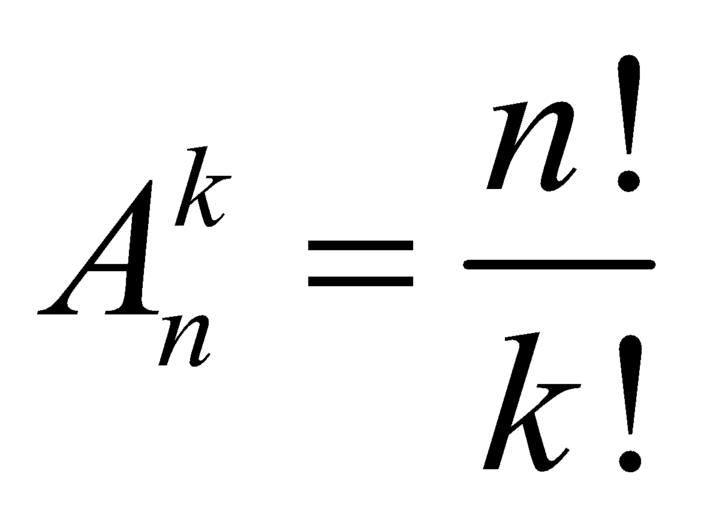 .
.
B. 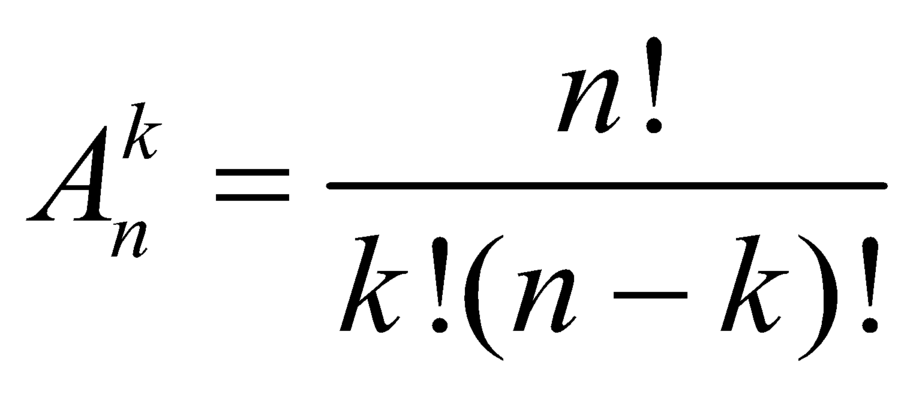 .
.
C. ![]()
D.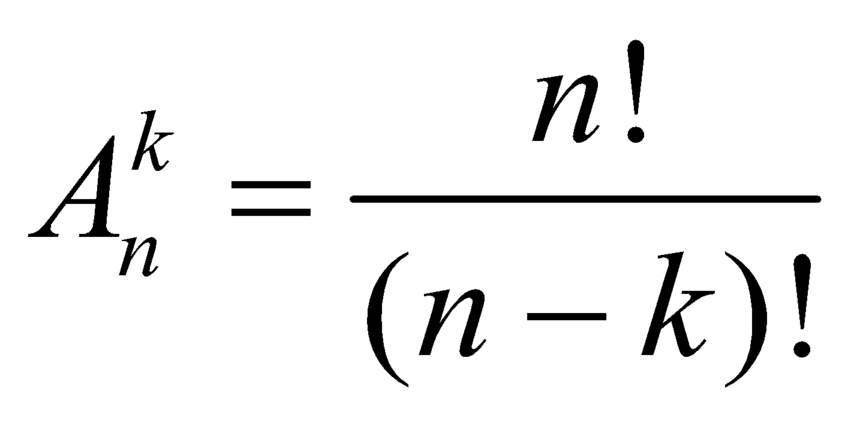 .
.
Cho
A
3
;
1
;
-
4
và
d
:
x
-
1
k
y
1
-
k
z
+
2
-...
Đọc tiếp
Cho A 3 ; 1 ; - 4 và d : x - 1 k = y 1 - k = z + 2 - 2 + k (k là tham số). Xác định k để khoảng cách từ A tới (d) đạt GTLN
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho ba đường thẳng
d
:
x
1
y
1
z
+
1
-
2
,
∆
1
:...
Đọc tiếp
Trong không gian Oxyz cho ba đường thẳng
d : x 1 = y 1 = z + 1 - 2 ,
∆ 1 : x - 3 2 = y 1 = z - 1 1 ,
∆ 2 : x - 1 1 = y - 2 2 = z 1 .
Đường thẳng ∆ vuông góc với d đồng thời cắt ∆ 1 , ∆ 2 tương ứng tại H, K sao cho độ dài HK nhỏ nhất.
Biết rằng ∆ có một vectơ chỉ phương u → = ( h ; k ; 1 ) Giá trị bằng h - k
A. 0
B. 4
C. 6
D. -2
Cho số phức z thỏa mãn
z
-
1
2
-
i
+
i
5
. Biết rằng tập hợp biểu diễn số phức w (1-i)z + 2i có dạng...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 2 - i + i = 5 . Biết rằng tập hợp biểu diễn số phức w = (1-i)z + 2i có dạng ( x + 2 ) 2 + y 2 = k Tìm k.
A. k = 92
B. k = 92
C. k = 50
D. k = 96
Cho đồ thị
(
C
)
:
y
2
x
-
3
x
-
2
và đường thẳng (d): 5x + y - 1 0 . Goi k là số tiếp tuyến của (C) vuông góc với (d). Xác định k.
Đọc tiếp
Cho đồ thị ( C ) : y = 2 x - 3 x - 2 và đường thẳng (d): 5x + y - 1 = 0 . Goi k là số tiếp tuyến của (C) vuông góc với (d). Xác định k.
![]()
![]()
![]()




