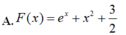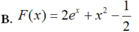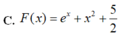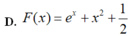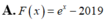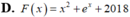Question

tìm nguyên hàm F(x) của hàm số f(x) thỏa mãn điều kiện tương ứng

a) \(f\left(x\right)=5^{2x}.2^x\) và F(0)=13

b) \(f\left(x\right)=3^x.2^{2x}\) và F(0)=12

Answer 1

a: \(f\left(x\right)=5^{2x}\cdot2^x=50^x\)

=>\(F\left(x\right)=\int50^xdx=\dfrac{50^x}{ln50}+C\)

F(0)=13

=>\(\dfrac{50^0}{ln50}+C=13\)

=>\(C=13-\dfrac{1}{ln50}\)

=>\(F\left(x\right)=\dfrac{50^x}{ln50}+13-\dfrac{1}{ln50}\)

b: \(f\left(x\right)=3^x\cdot2^{2x}=3^x\cdot4^x=12^x\)

=>\(F\left(x\right)=\int f\left(x\right).dx=\int12^xdx=\dfrac{12^x}{ln12}+C\)

F(0)=12

=>\(\dfrac{12^0}{ln12}+C=12\)

=>\(C=12-\dfrac{1}{ln12}\)

=>\(F\left(x\right)=\dfrac{12^x}{ln12}+12-\dfrac{1}{ln12}\)