Ta có: (x – 1)(x2 + 1) = 0
Vì x2 ≥ 0 với mọi giá trị của x ∈ R nên:
x2 + 1 > 0 với mọi x ∈ R
Suy ra: (x – 1)(x2 + 1) = 0 ⇔ x – 1 = 0 ⇔ x = 1
Vậy x = 1 là nghiệm của đa thức (x – 1)(x2 + 1)
Tìm nghiệm của các đa thức sau:
x2 - 2
x(x - 2)
x2 - 2x
x(x2 + 1)
1/ Tìm nghiệm của các đa thức x2 + x.
chứng tỏ rằng đa thức sau không có nghiệm: A(x) = x2 - 4x 7
Tìm nghiệm của đa thức sau: P (x) = x4 x3 x 1
Tìm nghiệm của các đa thức sau: x2 – x
Trong số các số bên phải của các đa thức sau, số nào là nghiệm của đa thức bên trái nó?
Q x = x 2 + x ; - 1 0 1 2 1
Trong số các số bên phải của các đa thức sau, số nào là nghiệm của đa thức bên trái nó?
M(x) = x 2 - 3 x + 2 ; - 2 - 1 1 2
Tìm nghiệm của các đa thức sau:
a. 2x + 10
b. 3x - 1/2
c. x2 – x
Trong các số cho sau, với mỗi đa thức, số nào là nghiệm của đa thức ?
a) P(x) = 2x +  |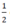
 |
 |
 |
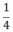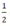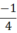| b) Q(x) = x2 – 2x -3 | 3 | 1 | -1 |
Bài 1: Cho hai đa thức:
P(x) = x2 + 5x4 – 3x3 + x2 - 5x4 + 3x3 – x + 5
Q(x) = x - 5x3– x2 + 5x3 - x2 + 3x – 1
a) Thu gọn rồi sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến.
b) Tính P(x) + Q(x) và P(x) - Q(x)
c) Tìm nghiệm của đa thức P(x) + Q(x)
