Đáp án B
Đồ thị hàm số y = a x = f x và y = 1 a x = a − x = f − x 0 < a ≠ 1 đối xứng nhau qua trục tung
Đáp án B
Đồ thị hàm số y = a x = f x và y = 1 a x = a − x = f − x 0 < a ≠ 1 đối xứng nhau qua trục tung
Cho 2 hàm số y = f x = log a x ; y = g x = a x . Xét các mệnh đề sau:
I. Đồ thị của hai hàm số f x , g x luôn cắt nhau tại một điểm
II. Hàm số f x + g x đồng biến khi a > 1 , nghịch biến khi 0 < a < 1
III. Đồ thị hàm số f x nhận trục Oy làm tiệm cận
IV. Chỉ có đồ thị hàm số f x có tiệm cận
Số mệnh đề đúng là
A. 1
B. 4
C. 2
D. 3
Cho hàm số y = f ( x ) có đạo hàm trên khoảng a ; b . Xét các mệnh đề sau:
I. Nếu hàm số y = f ( x ) đồng biến trên khoảng a ; b thì f ' x > 0 , ∀ x ∈ a ; b .
II. Nếu f ' x < 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) nghịch biến trên khoảng a ; b .
III. Nếu hàm số y = f ( x ) liên tục trên a ; b và f ' x > 0 , ∀ x ∈ a ; b thì hàm số y = f ( x ) đồng biến trên đoạn a ; b .
Số mệnh đề đúng là:
A. 3
B. 0
C. 2
D. 1
Cho hàm số y = x 3 − 6 x 2 + 9 x − 1 và các mệnh đề sau:
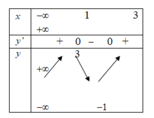
(1) Hàm số đồng biến trên các khoảng − ∞ ; 1 và 3 ; + ∞
nghịch biến trên khoảng (1;3)
(2) Hàm số đạt cực đại tại x = 3và x = 1
(3) Hàm số có y C D + 3 y C T = 0
(4) Hàm số có bảng biến thiên và đồ thị như hình vẽ.
Tìm số mệnh đề đúng trong các mệnh đề trên.
A. 1
B. 4
C. 2
D. 3
Cho a là một số thực dương khác 1. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau:
1. Hàm số y= l o g a x có tập xác định là D= ( 0 ; + ∞ ) .
2. Hàm số y= l o g a x là hàm đơn điệu trên khoảng ( 0 ; + ∞ ) .
3. Đồ thị hàm số y= l o g a x và đồ thị hàm số y = a x đối xứng nhau qua đường thẳng y= x.
4. Đồ thị hàm số y= l o g a x nhận Ox là một tiệm cận
A. 4
B. 1
C. 3
D. 2
Cho hai hàm số f ( x ) = log 2 x , g ( x ) = 2 x . Xét các mệnh đề sau:
I. Đồ thị hàm số đối xứng với nhau qua đường thẳng y=x
II. Tập xác định của hai hàm số trên là R
III. Đồ thị hai hàm số cắt nhau tại đúng 1 điểm
IV. Hai hàm số đều đồng biến trên tập xác định của nó
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên
A. 2
B. 3
C. 1
D. 4
Cho hai hàm số
f
x
=
log
0
,
5
x
và
g
x
=
2
−
x
. Xét các mệnh đề sau
(I) Đồ thị hàm số đối xứng nhau qua các đường thẳng y=-x
(II) Tập xác định của hai hàm số trên là R
(III) Đồ thị của hai hàm số cắt nhau tại đúng một điểm
(IV) Hai hàm số đều nghịch biến trên tập xác định của nó
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên
A. 3
B. 2
C. 1
D. 4
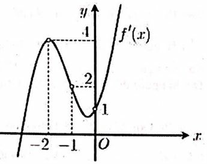
Cho hàm số y=f(x) có đồ thị đạo hàm y=f’(x) được cho như hình vẽ bên và các mệnh đề sau:
(1). Hàm số y=f(x) có duy nhất 1 điểm cực trị
(2). Hàm số y=f(x) nghịch biến trên khoảng (-2;1)
(3). Hàm số y=f(x) đồng biến trên khoảng 0 ; + ∞
(4). Hàm số g x = f x + x 2 có 2 điểm cực trị.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho hàm số f x = log 2 x , g x = 2 x . Xét các mệnh đề sau:
(I) Đồ thị hai hàm số đối xứng nhau qua đường thẳng y = x
(II) Tập xác định của hai hàm số trên là ℝ
(III) Đồ thị hai hàm số cắt nhau tại đúng 1 điểm.
(IV) Hai hàm số đều đồng biến trên tập xác định của nó.
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 2
B. 3
C. 1
D. 4
Cho hai hàm số y = e x và y = ln x . Xét các mệnh đề sau
(I) Đồ thị hai hàm số đối xứng qua đường thẳng y=x
(II) Tập xác định của hai hàm số trên là R
(III) Đồ thị hai hàm số cắt nhau tại đúng một điểm.
(IV) Hai hàm số đều đồng biến trên tập xác định của nó.
Có bao nhiêu mệnh đề sai trong các mệnh đề trên?
A. 2
B. 3
C. 1
D. 4
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có đồ thị hàm số y=f' (x) như hình vẽ bên. Xét hàm số g(x)=f(x^2-3) và các mệnh đề sau:

1. Hàm số g(x) có 3 điểm cực trị.
2. Hàm số g(x)đạt cực tiểu tại x = 0.
3. Hàm số g(x)đạt cực đại tại x = 2.
4. Hàm số g(x)đồng biến trên khoảng (-2;0).
5. Hàm số g(x)nghịch biến trên khoảng (-1;1).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 1.
B. 4.
C. 3.
D. 2.