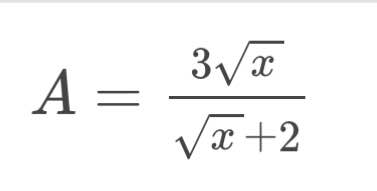Có: \(\dfrac{\sqrt{x}+3}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2+1}{\sqrt{x}+2}=1+\dfrac{1}{\sqrt{x}+2}\left(đk:x\ne4\right)\)
Để \(\dfrac{\sqrt{x}+3}{\sqrt{x}+2}\) lớn nhất thì \(\dfrac{1}{\sqrt{x}+2}\) lớn nhất
\(\Rightarrow\sqrt{x}+2\) nhỏ nhất
mà \(\sqrt{x}+2\ge2\)
\(\Rightarrow\dfrac{1}{\sqrt{x}+2}\le\dfrac{1}{2}\)
Dấu ''='' xảy ra khi \(\sqrt{x}+2=2\Rightarrow x=0\)
\(\Rightarrow B_{min}=1+\dfrac{1}{2}=\dfrac{3}{2}\)
\(B=\dfrac{\sqrt{x}+3}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2+1}{\sqrt{x}+2}=1+\dfrac{1}{\sqrt{x}+2}\)
Vì \(\sqrt{x}+2\ge2\Rightarrow\dfrac{1}{\sqrt{x+2}}\le\dfrac{1}{2}\Rightarrow1+\dfrac{1}{\sqrt{x}+2}\le1+\dfrac{1}{2}=\dfrac{3}{2}\)
\(\Rightarrow B\le\dfrac{3}{2}.MaxC=\dfrac{3}{2}\) khi x = 0