đúng nhé. em dựa theo lý thuyết bên trên ấy nhé
\(y'=3x^2-6x+m\)
để hàm số đồng biến trên R thì y'>0 với mọi x thuộc R
suy ra \(\begin{cases}3>0\\\Delta=9-3m
Tìm m để hàm số y = x 3 + 2 x 2 - m x + 1 đồng biến trên R.
A. m < - 4 3
B. m ≤ - 4 3
C. m ≥ - 4 3
D. m > - 4 3
Tìm tất cả giá trị của tham số m để hàm số y = x 3 + 3 x 2 + m x - 1 đồng biến trên R
A. m ≤ 3
B. m ≤ -3
C. m ≥ 3
D. m ≥ -3
Cho hàm số y = m 3 x 3 − m x 2 + 3 x + 1 ( m là tham số thực ). Tìm giá trị nhỏ nhất của m để hàm số trên luôn đồng biến trên R .
A. m = 3
B. m = − 2
C. m = 1
D. m = 0
Tập các giá trị thực của tham số m để hàm số y = ln ( 3 x - 1 ) - m x + 2 đồng biến trên khoảng 1 2 ; + ∞ là:
A. 2 9 ; + ∞
B. - 4 3 ; + ∞
C. - 7 3 ; + ∞
D. - 1 3 ; + ∞
Cho hàm số y = m x − 2 m − 3 x − m với m là tham số. Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên khoảng ( 2 ; + ∞ ) . Tìm số phần tử của S
A. 3
B. 4
C. 5
D. 1
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 - 3 x 2 + m x - 3 đồng biến trên R.
A. m ≥ 3
B. m ≤ 3
C. m ≤ 2
D. m ≥ 2
Cho hàm số y=f(x) liên tục và có đạo hàm trên R. Biết hàm số f’(x) có đồ thị được cho trong hình vẽ. Tìm điều kiện của m để hàm số g(x)=f(2019)x – mx +2 đồng biến trên [0;1]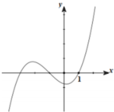
Tìm tất cả các giá trị của m để hàm số y = cos 2 x + m x đồng biến trên R.
A. 4
B. 2
C. 3
D. 1
Cho hàm số y = sin x - 3 cos x - m x . Tìm tất cả các giá trị thực của tham số m để hàm số đồng biến trên R
A. m ≤ - 2
B. m ≤ - 3
C. m ≥ 2
D. m ≥ 1
