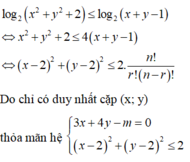Xét trên tập số tự nhiên
- Với \(y=0\Rightarrow\) ko tồn tại x thỏa mãn
- Với \(y=1\Rightarrow\) ko tồn tại x thỏa mãn
- Với \(y=2\Rightarrow x=1\)
- Với \(y\ge2\Rightarrow2^y⋮8\)
\(\Rightarrow5^x-1⋮8\)
Nếu \(x\) lẻ \(\Rightarrow x=2k+1\Rightarrow5^x=5.25^k\equiv5\left(mod8\right)\) \(\Rightarrow5^x-1\equiv4\left(mod8\right)\) ko chia hết cho 8 (ktm)
\(\Rightarrow x\) chẵn \(\Rightarrow x=2k\)
\(\Rightarrow5^x=5^{2k}=25^k\equiv1\left(mod3\right)\)
\(\Rightarrow5^x-1\equiv0\left(mod3\right)\Rightarrow5^x-1⋮3\Rightarrow2^y⋮3\) (vô lý)
Vậy với \(y\ge3\) ko tồn tại x;y thỏa mãn
Có đúng 1 cặp thỏa mãn là \(\left(x;y\right)=\left(1;2\right)\)