TXĐ: R \ {-3; 3}
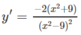
y' < 0 trên các khoảng (- ∞ ; - 3), (-3; 3), (3; + ∞ ) nên hàm số đã cho nghịch biến trên các khoảng đó.
TXĐ: R \ {-3; 3}
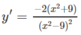
y' < 0 trên các khoảng (- ∞ ; - 3), (-3; 3), (3; + ∞ ) nên hàm số đã cho nghịch biến trên các khoảng đó.
Tìm các khoảng đồng biến nghịch biến của hàm số (x+3)sqrt(3-2x-x^2)
Phát biểu các điều kiện đồng biến và nghịch biến của hàm số. Tìm các khoảng đơn điệu của hàm số
y = - x 3 + 2 x 2 - x - 7 ; y = x - 5 1 - x
Tìm các khoảng đồng biến, nghịch biến của các hàm số: y = x 2 - 5 x + 3 x - 2
tìm khoảng đồng biến nghịch biến của hàm số sau
a) y = \(-x^4\) + \(8x^2\) + 1
b) y = \(x^4\) - 3
Tìm các khoảng đồng biến, nghịch biến của các hàm số: y = 1 x - 5 2
Tìm các khoảng đồng biến, nghịch biến của các hàm số: y = x 4 + 48 x
Tìm các khoảng đồng biến, nghịch biến của các hàm số: y = 3 - 2 x x + 7
Tìm các khoảng đồng biến, nghịch biến của các hàm số: y = x 2 - 2 x + 3 x + 1
Cho các khẳng định:
(I) : Hàm số y=2 đồng biến trên R.
(II) : Hàm số y = x 3 - 12 x nghịch biến trên khoảng (-1;2).
(III): Hàm số y = 2 x - 5 x - 2 đồng biến trên các khoảng - ∞ ; 2 và 2 ; + ∞ .
Trong các khẳng định trên có bao nhiêu khẳng định đúng?
![]()
![]()
![]()
![]()