Đáp án D
lim x → + ∞ 4 x 2 − x + 1 2 x + 1 = lim x → + ∞ 4 − 1 x + 1 x 2 2 + 1 x = 1
lim x → − ∞ 4 x 2 − x + 1 2 x + 1 = lim x → + ∞ − 4 − 1 x + 1 x 2 2 + 1 x = − 1
Đáp án D
lim x → + ∞ 4 x 2 − x + 1 2 x + 1 = lim x → + ∞ 4 − 1 x + 1 x 2 2 + 1 x = 1
lim x → − ∞ 4 x 2 − x + 1 2 x + 1 = lim x → + ∞ − 4 − 1 x + 1 x 2 2 + 1 x = − 1
Xét các mệnh đề sau
(1). Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
(2). Đồ thị hàm số y = x + x 2 + x + 1 x có hai đường tiệm cận ngang và một đường tiệm cận đứng
(3). Đồ thị hàm số y = x - 2 x - 1 x 2 - 1 có một đường tiệm cận ngang và hai đường tiệm cận đứng.
Số mệnh đề đúng là:
A. 0
B. 3
C. 2
D. 1
Cho hàm số y = x + 1 a x 2 + 1 có đồ thị (C). Tìm a để đồ thị hàm số có đường tiệm cận ngang và đường tiệm cận đó cách đường tiếp tuyến của (C) một khoảng bằng 2 - 1
A. a>0
B. a=2
C. a=3
D. a=1
Cho hàm số y=f(x) xác định, liên tục trên tập R\{1} và có bảng biến thiên
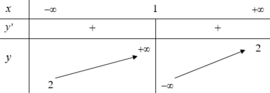
Số mệnh đề đúng trong các mệnh đề sau là?
1. Đường thẳng y=2 là đường tiệm cận ngang của đồ thị hàm số.
2. Đường thẳng x=1 là đường tiệm cận đứng của đồ thị hàm số.
3. Hàm số đồng biến trên các khoảng - ∞ ; 1 và 1 ; + ∞
A. 0.
B. 1
C. 2.
D. 3
Biết rằng các đường thẳng x=1,y=2 lần lượt là đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 2 a x + 1 x - b Tính giá trị T=a+b+ab
A. T=4.
B. T=0.
C. T=2.
D. T=3.
Cho hàm số y = x − 1 x − 3 . Xét các mệnh đề sau:
(1) Hàm số nghịch biến trên D = ℝ \ 3
(2) Đồ thị hàm số có một tiệm cận đứng là x=1, tiệm cận ngang là y=3.
(3) Hàm số đã cho không có cực trị
(4) Đồ thị hàm số nhận giao điểm I(3;1) của hai đường tiệm cận làm tâm đối xứng.
Chọn các mệnh đề đúng ?
A. (1), (3), (4)
B. (3), (4)
C. (2), (3), (4)
D. (1), (4)
Cho hàm số y = a x - 1 b x + 2 . Xác định a và b để đồ thị hàm số nhận đường thẳng x = 2 là tiệm cận đứng và đường thẳng y = - 1 làm tiệm cận ngang.
A. a = 2 , b = - 3
B. a = 2 , b = - 2
C. a - 1 , b = 1
D. a = 1 , b = - 1
Tìm số phát biểu đúng trong các phát biểu sau:
(1) Đồ thị hàm số y= x α với α > 0 nhận trục Ox làm tiệm cận ngang và nhận trục là tiệm cận đứng.
(2) Đồ thị hàm số y= x α với α > 0 không có tiệm cận.
(3) Đồ thị hàm số y = log a x với 1 < a ≠ 1 nhận trục Oy làm tiệm cận đứng và không có tiệm cận ngang.
(4) Đồ thị hàm số y=ax với 1 < a ≠ 1 nhận trục Ox làm tiệm cận ngang và không có tiệm cận đứng.
A. 2.
B. 1
C. 4
D. 3.
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số y = 3 x - 1 x - 2
A. x = 2
B. x = 3
C. y = 3
D. y = 2
Cho hàm số y = a x − b b x + 1 có đồ thị (C). Nếu (C) có tiệm cận ngang là đường thẳng y=2 và tiệm cận đứng là đường thẳng x = 1 3 thì các giá trị của a và b lần lượt là :
A. − 1 2 và − 1 6
B. -3 và -6
C. − 1 6 và − 1 2
D. -6 và -3
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 − 2 x − x + 2 là:
A. x = − 2 ; y = − 2
B. x = 2 ; y = − 2
C. x = − 2 ; y = 2
D. x = 2 ; y = 2