Chọn đáp án A
Ta có f 0 = 0 . Theo định nghĩa đạo hàm:
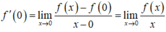
Suy ra
![]()
![]()
![]()
Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ x = 0 là
![]()
Chọn đáp án A
Ta có f 0 = 0 . Theo định nghĩa đạo hàm:
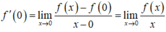
Suy ra
![]()
![]()
![]()
Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ x = 0 là
![]()
Cho hàm số y=f(x) có đạo hàm liên tục trên ( 0 ; + ∞ ) thỏa mãn f ' ( x ) + f ( x ) x = 4 x 2 + 3 x và f(1)=2. Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x = 2 là x
A. y = 16x+20.
B. y = -16x+20
C. y = -16x-20
D. y = 16x-20.
Cho hàm số y=f(x) có đồ thị là (C), hàm số y=f'(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x=2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,b
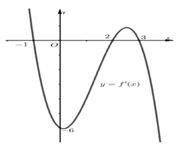
Giá trị ( a - b ) 2 thuộc khoảng nào dưới đây
A. ( 0 ; 9 )
B. ( 12 ; 16 )
C. ( 16 ; + ∞ )
D. ( 9 ; 12 )
Cho hai hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e với a ≠ 0 và g(x)= p x 2 + q x - 3 c ó đồ thị như hình vẽ bên dưới. Đồ thị hàm số y=f(x) đi qua gốc tọa độ và cắt đồ thị hàm số y=g(x) tại bốn điểm có hoành độ lần lượt là -2;-1;1 và m. Tiếp tuyến của đồ thị hàm số y=f(x)-g(x) tại điểm có hoành độ x=-2 có hệ số góc bằng -15/2. Gọi (H) là hình phẳng giới hạn bởi đồ thị hai hàm số y=f(x) và y=g(x) (phần được tô đậm trong hình vẽ). Diện tích của hình (H) bằng

A. 1553 120
B. 1553 240
C. 1553 60
D. 1553 30
Cho hàm số y=f(x) xác định, có đạo hàm trên R thỏa mãn f 2 ( - x ) = ( x 2 + 2 x + 4 ) f ( x + 2 ) và f ( x ) ≠ 0 , ∀ x ∈ R . Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=2 là
A. y=-2x+4.
B. y=2x+4.
C. y=2x.
D. y=4x+4.
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số y=f(x) có đạo hàm f '(x) trên R thỏa mãn f 2 1 + 2 x = x − f 3 1 − x . Tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x=1 là
A. y = − 1 7 x − 6 7 .
B. y = 1 7 x − 8 7 .
C. y = − 1 7 x + 8 7 .
D. y = − x + 6 7 .
Cho 3 hàm số y=f(x), y=g(x), y = f ( x ) + 3 g ( x ) + 3 . Biết hệ số góc các tiếp tuyến của đồ thị các hàm số đã cho tại điểm có hoành độ x=1 là bằng nhau và khác 0. Mệnh đề nào dưới đây đúng
A. f ( 1 ) ≤ - 11 4
B. f ( 1 ) < - 11 4
C. f ( 1 ) > - 11 4
D. f ( 1 ) ≥ - 11 4
Cho hàm số y = f (x) có đồ thị (C), biết tiếp tuyến của đồ thị (C) tại điểm có hoành độ
x = 0 là đường thẳng y = 3x - 3. Giá trị của lim x → 0 3 x f ( 3 x ) − 5 f ( 4 x ) + 4 f ( 7 x )
A. 1 10
B. 3 31
C. 3 25
D. 1 11
Phương trình tiếp tuyến của đồ thị hàm số y = x + x 2 + 1 tại điểm có hoành độ x = 0 là:
A. y = x + 1
B. y = x + 2
C. y = x - 1
D. y = x - 2