Chọn A.
Đặt t = x + 1⇒ dt = dx. Đổi cận: x = 0 ⇒ t = 1; x = 1 ⇒ t = 2
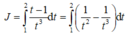
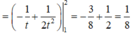
Chọn A.
Đặt t = x + 1⇒ dt = dx. Đổi cận: x = 0 ⇒ t = 1; x = 1 ⇒ t = 2
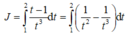
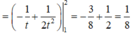
Cho I = lim x → 0 2 x + 1 − 1 x và J = lim x → 1 x 2 + x − 2 x − 1 . Tính I+J
A. 3
B. 5
C. 4
D. 2
Cho I = ∫ 1 5 f ( x ) d x = 26 . Khi đó J = ∫ 0 2 x . [ f ( x 2 + 1 ) + 1 ] d x bằng
![]()
![]()
![]()
![]()
Cho tích phân I = ∫ 0 2 f ( x ) d x = 2 . Tính tích phân J = ∫ 0 2 3 f ( x ) - 2 d x
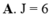
![]()
![]()
![]()
Tính tích phân sau J = ∫ 2 7 x d x x + 2 + x - 2
A. 19 - 5 5 9
B. 19 - 5 5 3
C. 19 - 5 5 6
D. 3.
Cho A(2;3;-1) B(-1;1;1) C(3;5;2)
1)Tìm độ dài đường cao AH
2)Tìm J \(\in\) Oz để A,B,J thẳng hàng
Cho tích phân I = ∫ 0 4 f ( x ) d x = 32 . Tính tích phân J = ∫ 0 2 f ( 2 x ) d x
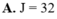
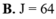
![]()
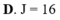
Tính tích phân sau : J = ∫ 0 2 π ln sin x + 1 + sin 2 x d x
A. 0
B. 1
C. 2
D. 3
1!x2!x3!x4!x5!x6!x..............x999!=?
Cho mk hỏi url youtube là j
Cho I = ∫ 0 1 2 x 2 - x - m d x và J = ∫ 0 1 x 2 - 2 m x d x . Tìm điều kiện của tham số thực m để I ≤ J .
A. m ≥ 2
B. m ≥ 3
C. m ≥ 0
D. m ≥ 1
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$