Các câu hỏi tương tự
Để tiết kiệm vật liệu nhất thì
S
t
p
nhỏ nhất
⇔
πR
2
π
R
⇒
R
1
⇒
h
2
Cho đồ thị hàm số yf(x) như hình vẽ dưới đây: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số
y
f
(
x...
Đọc tiếp
Để tiết kiệm vật liệu nhất thì S t p nhỏ nhất ⇔ πR 2 = π R ⇒ R = 1 ⇒ h = 2 Cho đồ thị hàm số y=f(x) như hình vẽ dưới đây:
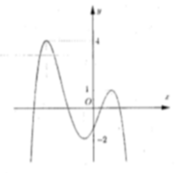
Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f ( x - 2 ) - m 4 có 7 điểm cực trị.
A. 1
B. 2
C. 3
D. 4
Tính thể tích V của khối nón có bán kính đáy r = 3 và chiều cao h = 4
A. V = 4 π
B. V = 12 π
C. V = 16 π 3
D. V = 4
Cho khối nón có bán kính đáy
r
3
và chiều cao h 4. Tính thể tích V của khối nón đã cho. A.
V
16
π
3
B.
V
12
π
C.
V
4
D.
V
4
π
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao h= 4. Tính thể tích V của khối nón đã cho.
A. V = 16 π 3
B. V = 12 π
C. V = 4
D. V = 4 π
Cho khối nón có bán kính đáy
r
3
và chiều cao h4. Tính thể tích V của khối nón đã cho A.
V
4
π
B.
V
5
π
C.
V
6
π
D.
V
7
π
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao h=4. Tính thể tích V của khối nón đã cho
A. V = 4 π
B. V = 5 π
C. V = 6 π
D. V = 7 π
Cho khối nón có bán kính đáy
r
3
và chiều cao h 4. Tính thể tích V của khối nón đã cho. A.
V
16
π
3
3
B.
V
4
π
C.
V
16
π
3
D.
V
12
π
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao h = 4. Tính thể tích V của khối nón đã cho.
A. V = 16 π 3 3
B. V = 4 π
C. V = 16 π 3
D. V = 12 π
Cho khối nón có bán kính đáy
r
3
và chiều cao h 4. Tính thể tích V của khối nón đã cho. A.
V
12
π
B.
V
4
π
C. V4 D. V12
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao h = 4. Tính thể tích V của khối nón đã cho.
A. V = 12 π
B. V = 4 π
C. V=4
D. V=12
Cho khối nón có bán kính đáy
r
3
và chiều cao
h
4.
Tính thể tích V của khối nón đã cho. A.
V
16
π
3
B.
V
16
π
C.
V
4
D.
V
4
π
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao h = 4. Tính thể tích V của khối nón đã cho.
A. V = 16 π 3
B. V = 16 π
C. V = 4
D. V = 4 π
Cho khối nón có bán kính đáy r 3, chiều cao
h
2
Tính thể tích V của khối nón. A.
V
3
π
2
3
B.
V
3
π
2
C.
V
9
π
2
3
D.
V...
Đọc tiếp
Cho khối nón có bán kính đáy r = 3, chiều cao h = 2 Tính thể tích V của khối nón.
A. V = 3 π 2 3
B. V = 3 π 2
C. V = 9 π 2 3
D. V = 9 π 2
Cho hình trụ có bán kính đáy r = 3 và diện tích xung quanh S = 6π. Thể tích V của khối trụ là:
A. V = 3π
B. V = 9π
C. V = 18π
D. V = 6π
Cho khối nón có bán kính r 5 và chiều cao h 3 Tính thể tích V của khối nón A.
V
9
π
5
B.
V
3
π
5
C.
V
π
5
D.
V
5
π
Đọc tiếp
Cho khối nón có bán kính r = 5 và chiều cao h = 3 Tính thể tích V của khối nón
A. V = 9 π 5
B. V = 3 π 5
C. V = π 5
D. V = 5 π



